
 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.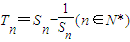 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值. 的等比数列{an}不是递减数列,求出q值,可得答案.
的等比数列{an}不是递减数列,求出q值,可得答案. 在n为奇数和偶数时的范围,综合讨论结果,可得答案.
在n为奇数和偶数时的范围,综合讨论结果,可得答案. =
=


 ×(-
×(- )n-1=(-1)n-1•
)n-1=(-1)n-1•
 )n=
)n=

 ≤
≤ =
= -
- =
=

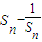 ≥
≥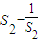 =
= -
- =
=
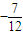 ≤
≤ ≤
≤
 ,最小项的值为
,最小项的值为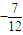


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年四川绵阳高中高三第二次诊断性考试理科数学试卷(解析版) 题型:解答题
已知首项为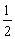 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若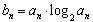 ,数列{bn}的前n项和Tn,求满足不等式
,数列{bn}的前n项和Tn,求满足不等式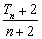 ≥
≥ 的最大n值.
的最大n值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川绵阳高中高三第二次诊断性考试文科数学试卷(解析版) 题型:解答题
已知首项为 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知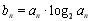 ,求数列{bn}的前n项和
,求数列{bn}的前n项和 .
.
查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试文科数学(天津卷解析版) 题型:解答题
已知首项为 的等比数列
的等比数列 的前n项和为
的前n项和为 , 且
, 且 成等差数列.
成等差数列.
(Ⅰ) 求数列 的通项公式;
的通项公式;
(Ⅱ) 证明 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知首项为![]() 的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
(1)求数列{an}的通项公式.
(2)证明Sn+![]() ≤
≤![]() (n∈N*).
(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com