
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(Ⅲ)在(Ⅰ)的条件下,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 时,
时, ![]() 在
在![]() 无零点;
无零点; ![]() 时,
时, ![]() 在
在![]() 恰有一个零点;
恰有一个零点; ![]() 时,
时, ![]() 在
在![]() 有两个零点(3)
有两个零点(3)![]() 或
或![]()
【解析】试题分析:(1)利用导数的几何意义,得![]() ,
, ![]() ;(2)函数的零点个数等价于两个函数的交点的个数,即
;(2)函数的零点个数等价于两个函数的交点的个数,即![]() 与
与![]() 的交点个数;(3)不等式能成立问题转化为函数的最值问题.
的交点个数;(3)不等式能成立问题转化为函数的最值问题.
试题解析:
(Ⅰ)![]() ,函数
,函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线
![]() .
.![]() .
.
(Ⅱ)令![]()
![]() ,
, ![]() 得
得![]()
记![]()
![]() ,
, ![]() 由此可知
由此可知
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
且![]()
![]()
![]() 时
时![]()
故![]() 时,
时, ![]() 在
在![]() 无零点
无零点
![]() 时,
时, ![]() 在
在![]() 恰有一个零点
恰有一个零点
![]() 时,
时, ![]() 在
在![]() 有两个零点
有两个零点
(Ⅲ)在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立等价于函数
成立等价于函数![]() 在
在![]() 上的最小值小于零.
上的最小值小于零.
![]() ,
,
①当![]() 时,即
时,即![]() 时,
时, ![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 的最小值为
的最小值为![]() ,由
,由![]() 可得
可得![]() ,
,![]() ;
;
②当![]() 时,即
时,即![]() 时,
时, ![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 的最小值为
的最小值为![]() ,由
,由![]() 可得
可得![]() ;
;
③当![]() 时,即
时,即![]() 时,可得
时,可得![]() 的最小值为
的最小值为![]() 此时,
此时, ![]() 不成立.
不成立.
综上所述:可得所求![]() 的范围是
的范围是![]() 或
或![]()


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】设△ABC的三内角A、B、C的对边分别是a、b、c,且b(sinB﹣sinC)+(c﹣a)(sinA+sinC)=0 (Ⅰ)求角A的大小;
(Ⅱ)若a= ![]() ,sinC=
,sinC= ![]() sinB,求△ABC的面积.
sinB,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 是奇函数,f(x)=lg(10x+1)+bx是偶函数.
是奇函数,f(x)=lg(10x+1)+bx是偶函数.
(1)求a和b的值.
(2)说明函数g(x)的单调性;若对任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求实数k的取值范围.
(3)设 ![]() ,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:sin230°+sin290°+sin2150°= ![]() ;
;
sin25°+sin265°+sin2125°= ![]() ;
;
sin212°+sin272°+sin2132°= ![]() ;
;
通过观察上述两等式的规律,请你写出一般性的命题,并给予的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.71828…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.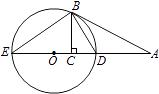
(1)证明:∠CBD=∠DBA;
(2)若AD=3DC,BC= ![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点. 
(1)求证:VD∥平面EAC;
(2)求二面角A﹣VB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)在x= ![]() 处取得最大值,则函数y=f(x+
处取得最大值,则函数y=f(x+ ![]() )是( )
)是( )
A.奇函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点( ![]() ,0)对称
,0)对称
C.奇函数且它的图象关于点( ![]() ,0)对称
,0)对称
D.偶函数且它的图象关于点(π,0)对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com