
【题目】已知函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 存在极大值,且极大值点为1,证明:
存在极大值,且极大值点为1,证明: ![]() .
.
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2-5x+b>0的解是-3<x<2,设A={x|bx2-5x+a>0},B={x|![]() }.
}.
(1)求a,b的值;
(2)求A∩B和A∪(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,左顶点为
,左顶点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,对于任意的
,对于任意的![]() 都有
都有![]() ,若存在,求出点
,若存在,求出点![]() 的
的
坐标;若不存在说明理由;
(3)若过![]() 点作直线
点作直线![]() 的平行线交椭圆
的平行线交椭圆![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几千年的沧桑沉淀,凝练了西樵山的美,清幽秀丽的自然风光,文化底蕴厚重的旅游,古朴自然的民俗风情.自明清以来,文人雅士,群贤毕至,旅人游子,纷至沓来,使秀美的西樵山成为名嗓南粤的旅游热点.如图,游客从某旅游景区的景点![]() 处下山至
处下山至![]() 处有两种路径,一种是从
处有两种路径,一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 乘景区观光车到
乘景区观光车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从
匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从![]() 乘观光车到
乘观光车到![]() ,在
,在![]() 处停留20分钟后,再从
处停留20分钟后,再从![]() 匀速步行到
匀速步行到![]() .假设观光车匀速直线运行的速度为250米/分钟,山路
.假设观光车匀速直线运行的速度为250米/分钟,山路![]() 长为2340米,经测量,
长为2340米,经测量,![]() ,
,![]() .
.
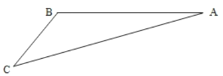
(1)求观光车路线![]() 的长;
的长;
(2)问乙出发多少分钟后,乙在观光车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在R上的增函数,则下列结论一定正确的是( )
A.f(x)+f(-x)是偶函数且是增函数
B.f(x)+f(-x)是偶函数且是减函数
C.f(x)-f(-x)是奇函数且是增函数
D.f(x)-f(-x)是奇函数且是减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com