
分析 (1)m∈{x|0≤x≤3,x∈N*}={1,2,3},n∈{x|0≤x≤2,x∈Z}={0,1,2},基本事件总数为9,△>0,m2+n2>4,求出满足条件的(m,n)的个数,即可求出方程有两个不相等实根的概率;
(2)m∈{x|0≤x≤3,x∈R},n∈{x|0≤x≤2,x∈R},对应区域的面积为6,△≥0,m2+n2≥4,对应区域的面积为6-$\frac{1}{4}π•4$=6-π,即可求出方程有实数根的概率.
解答 解:方程的△=36m2+36(n2-4).
(1)m∈{x|0≤x≤3,x∈N*}={1,2,3},n∈{x|0≤x≤2,x∈Z}={0,1,2},基本事件总数为9
△>0,m2+n2>4,满足条件的(m,n)为(1,2),(2,1),(2,2),(3,0),(3,1),(3,2),共6个,
∴方程有两个不相等实根的概率为$\frac{6}{9}$=$\frac{2}{3}$;
(2)m∈{x|0≤x≤3,x∈R},n∈{x|0≤x≤2,x∈R},对应区域的面积为6,
△≥0,m2+n2≥4,对应区域的面积为6-$\frac{1}{4}π•4$=6-π,
∴方程有实数根的概率为$\frac{6-π}{6}$=1-$\frac{π}{6}$.
点评 本题考查几何概型,考查方程根的研究,正确确定测度是关键.


科目:高中数学 来源: 题型:选择题
| A. | y=2-x | B. | y=x-$\frac{1}{x}$ | C. | y=-$\frac{1}{{x}^{2}}$ | D. | y=-tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k<-1 | B. | k≤-1 | C. | k>2 | D. | k≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
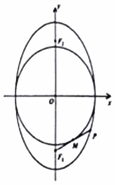 若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点.
若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
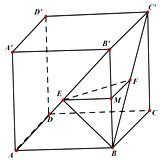 如图,在正方体ABCD-A'B'C'D'中,E,F分别是AB',BC'的中点.
如图,在正方体ABCD-A'B'C'D'中,E,F分别是AB',BC'的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象(如图所示),则f(x)的解析式为$y=2sin(2x+\frac{π}{6})$.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象(如图所示),则f(x)的解析式为$y=2sin(2x+\frac{π}{6})$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com