
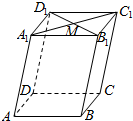
 如图,已知平行六面体ABCD-A1B1C1D1,M为A1C1与B1D1的交点,化简下列向量表达式:
如图,已知平行六面体ABCD-A1B1C1D1,M为A1C1与B1D1的交点,化简下列向量表达式:分析 类比平面向量的线性运算法则,结合平行六面体的性质,对下列各式进行化简即可.
解答 解:如图所示, 平行六面体ABCD-A1B1C1D1中,
平行六面体ABCD-A1B1C1D1中,
(1)$\overrightarrow{A{A}_{1}}$+$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{{AB}_{1}}$;
(2)$\frac{1}{2}$$\overrightarrow{{A}_{1}{B}_{1}}$+$\frac{1}{2}$$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\frac{1}{2}$($\overrightarrow{{{A}_{1}B}_{1}}$+$\overrightarrow{{{A}_{1}D}_{1}}$)
=$\frac{1}{2}$$\overrightarrow{{{A}_{1}C}_{1}}$=$\overrightarrow{{A}_{1}M}$;
(3)$\overrightarrow{A{A}_{1}}$+$\frac{1}{2}$$\overrightarrow{{A}_{1}{B}_{1}}$+$\frac{1}{2}$$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{{AA}_{1}}$+$\frac{1}{2}$($\overrightarrow{{{A}_{1}B}_{1}}$+$\overrightarrow{{{A}_{1}D}_{1}}$)
=$\overrightarrow{{AA}_{1}}$+$\frac{1}{2}$$\overrightarrow{{{A}_{1}C}_{1}}$
=$\overrightarrow{{AA}_{1}}$+$\overrightarrow{{A}_{1}M}$
=$\overrightarrow{AM}$;
(4)$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$+$\overrightarrow{{C}_{1}{A}_{1}}$+$\overrightarrow{{A}_{1}A}$=$\overrightarrow{AC}$+$\overrightarrow{{CC}_{1}}$+$\overrightarrow{{{C}_{1}A}_{1}}$+$\overrightarrow{{A}_{1}A}$
=$\overrightarrow{{AC}_{1}}$+$\overrightarrow{{{C}_{1}A}_{1}}$+$\overrightarrow{{A}_{1}A}$
=$\overrightarrow{{AA}_{1}}$+$\overrightarrow{{A}_{1}A}$
=$\overrightarrow{0}$.
点评 本题考查了空间向量的线性表示与运算问题,是基础题目.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | {α|α=475°+k•360°,k∈Z} | B. | α|α=97°+k•360°,k∈Z} | ||
| C. | α|α=263°+k•360°,k∈Z} | D. | α|α=-263°+k•360°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
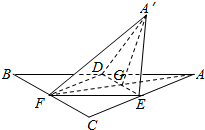 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有DE⊥平面A′GF | |
| C. | 三棱锥A′-FED的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
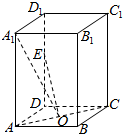 如图所示,在长方体体ABCD-A1B1C1D1中,O为AC的中点.
如图所示,在长方体体ABCD-A1B1C1D1中,O为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com