
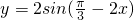 的单调递减区间是________.
的单调递减区间是________.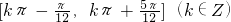
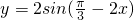 化为y=-2sin(2x-
化为y=-2sin(2x- )因此要求函数
)因此要求函数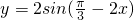 的单调递减区间即求y=2sin(2x-
的单调递减区间即求y=2sin(2x- )的单调递增区间,故可将2x-
)的单调递增区间,故可将2x- 看成整体然后正弦函数的递增区间求不等式2kπ-
看成整体然后正弦函数的递增区间求不等式2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ 的解集即可.
的解集即可.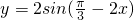
 )
)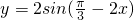 的单调递减区间即求y=2sin(2x-
的单调递减区间即求y=2sin(2x- )的单调递增区间
)的单调递增区间 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z
,k∈z ≤x≤kπ
≤x≤kπ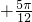 ,k∈z
,k∈z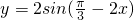 的单调递减区间是[kπ-
的单调递减区间是[kπ- ,k
,k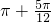 ](k∈z)
](k∈z)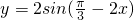 的单调递减区间.解题的关键是要注意正弦函数的自变量x的系数为正因此需利用诱导公式可将函数
的单调递减区间.解题的关键是要注意正弦函数的自变量x的系数为正因此需利用诱导公式可将函数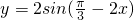 的自变量x的系数为正即y=-2sin(2x-
的自变量x的系数为正即y=-2sin(2x- ),然后要分析出函数
),然后要分析出函数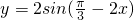 的单调递减区间即求y=2sin(2x-
的单调递减区间即求y=2sin(2x- )的单调递增区间,最后一定不要忘记k∈z!
)的单调递增区间,最后一定不要忘记k∈z! 

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com