练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若x1满足2x+2x=5，x2满足2x+2log2（x﹣1）=5，x1+x2=（ ）
    A.
    B.3
    C.
    D.4

    【答案】C
    【解析】解：由题意 ①

    2x2+2log2（x2﹣1）=5 ②

    所以 ，

    x1=log2（5﹣2x1） 即2x1=2log2（5﹣2x1）

    令2x1=7﹣2t，代入上式得7﹣2t=2log2（2t﹣2）=2+2log2（t﹣1）

    ∴5﹣2t=2log2（t﹣1）与②式比较得t=x2

    于是2x1=7﹣2x2

    即x1+x2=

    故选C

    先由题中已知分别将x1、x2所满足的关系表达为，2x1=2log2（5﹣2x1）…系数配为2是为了与下式中的2x2对应

    2x2+2log2（x2﹣1）=5，观察两个式子的特点，发现要将真数部分消掉求出x1+x2，只须将5﹣2x1化为2（t﹣1）的形式，则2x1=7﹣2t，t=x2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设命题p：x2﹣4ax+3a2＜0（其中a＞0，x∈R），命题q：﹣x2+5x﹣6≥0，x∈R．
    （1）若a=1，且p∧q为真，求实数x的取值范围；
    （2）若￢p是￢q的充分不必要条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=1﹣ （a＞0且a≠1）是定义在R上的奇函数． （Ⅰ）求a的值；
    （Ⅱ）若关于x的方程|f（x）（2x+1）|=m有1个实根，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=loga（ax+1）+mx是偶函数．
    （1）求m；
    （2）当a＞1时，若函数f（x）的图象与直线l：y=﹣mx+n无公共点，求n的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】与圆（x+1）2+y2=1和圆（x﹣5）2+y2=9都相切的圆的圆心轨迹是（ ）
    A.椭圆和双曲线
    B.两条双曲线
    C.双曲线的两支
    D.双曲线的一支

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，抛物线关于x轴对称，它的顶点在坐标原点，点P（1，2），A（x1 ， y1），B（x2 ， y2）均在抛物线上．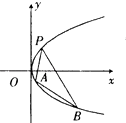

    （1）求该抛物线方程；
    （2）若AB的中点坐标为（1，﹣1），求直线AB方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x），（x∈R）上任一点（x0 ， y0）的切线方程为y﹣y0=（x0﹣2）（x02﹣1）（x﹣x0），那么函数f（x）的单调递减区间是（ ）
    A.[﹣1，+∞）
    B.（﹣∞，2]
    C.（﹣∞，﹣1）和（1，2）
    D.[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知过点P（m，n）的直线l与直线l0：x+2y+4=0垂直． （Ⅰ） 若 ，且点P在函数 的图象上，求直线l的一般式方程；
    （Ⅱ） 若点P（m，n）在直线l0上，判断直线mx+（n﹣1）y+n+5=0是否经过定点？若是，求出该定点的坐标；否则，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=x2﹣ax+1，x∈[﹣1，2]．
    （1）若函数f（x）为单调函数，求a的取值范围；
    （2）求函数f（x）的最小值．

    查看答案和解析>>

    同步练习册答案