练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知曲线的参数方程为：（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，直线的直角坐标方程为.

    （l）求曲线和直线的极坐标方程；

    （2）已知直线分别与曲线、曲线交异于极点的，若的极径分别为，求的值.

    【答案】(1)，；(2)3.

    【解析】

    （1）曲线为圆：，用公式代入，得极坐标方程,直线过原点，且倾斜角为，所以直线的极坐标方程为；（2）曲线均为圆且都过极点O，所以代入，分别求得极径分别为，代入即求解.

    （1）曲线的参数方程为（为参数），普通方程为，

    极坐标方程为，

    ∵直线的直角坐标方程为，

    故直线的极坐标方程为.

    （2）曲线的极坐标方程为：，

    直线的极坐标方程为，

    将代入的极坐标方程得，

    将代入的极坐标方程得，

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在三棱锥中， 和是边长为的等边三角形， ， 分别是的中点.

    （1）求证： 平面；

    （2）求证: 平面；

    （3）求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为定义在上的奇函数，且当时，

    （Ⅰ）求函数的解析式；

    （Ⅱ）求函数在区间 上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在边长为a的菱形ABCD中，，E,F分别是PA和AB的中点．

    （1）求证： EF||平面PBC；

    （2）求E到平面PBC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，摩天轮的半径为50m，圆心O距地面的高度为65m．已知摩天轮按逆时针方向匀速转动，每30min转动一圈．游客在摩天轮的舱位转到距离地面最近的位置进舱．

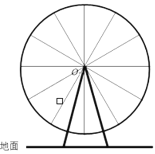
    （1）游客进入摩天轮的舱位，开始转动tmin后，他距离地面的高度为h，求h关于t的函数解析式；

    （2）已知在距离地面超过40m的高度，游客可以观看到游乐场全景，那么在摩天轮转动一圈的过程中，游客可以观看到游乐场全景的时间是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知多面体的底面是边长为的菱形， 底面， ，且．

    （1）证明：平面平面；

    （2）若直线与平面所成的角为，求二面角

    的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调性；

    （2）设，当时，对任意，存在，使，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义域为R的函数．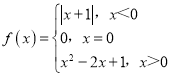

    （1）在平面直角坐标系中作出函数f（x）的图象，并指出f（x）的单调区间（不需证明）；

    （2）若方程f（x）+5a＝0有两个解，求出a的取值范围（不需严格证明，简单说明即可）；

    （3）设定义域为R的函数g（x）为偶函数，且当x≥0时，g（x）＝f（x），求g（x）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的右焦点与抛物线的焦点重合，且椭圆的离心率为．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设是椭圆的右顶点，过点作两条直线分别与椭圆交于另一点，若直线的斜率之积为，求证：直线恒过一个定点，并求出这个定点的坐标.

    查看答案和解析>>

    同步练习册答案