
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
分析 根据基本不等式的性质分别对①②③④进行判断即可.
解答 解:①x>0时,|x+$\frac{1}{x}$|=x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,
当且仅当x=1时,“=”成立,
x<0时,|x+$\frac{1}{x}$|=-x-$\frac{1}{x}$≥2$\sqrt{(-x)•(-\frac{1}{x})}$,
当且仅当x=-1时,“=”成立,
故①正确;
②$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$=$\frac{{x}^{2}+1+1}{\sqrt{{x}^{2}+1}}$=$\sqrt{{x}^{2}+1}$+$\frac{1}{\sqrt{{x}^{2}+1}}$≥2,
当且仅当x=0时,“=”成立,
故②正确;
③当0<x<1时,log2x+logx2的和是负数,
故③错误;
④3x+3-x=3x+$\frac{1}{{3}^{x}}$≥2$\sqrt{{3}^{x}•\frac{1}{{3}^{x}}}$=2,
当且仅当x=0时,“=”成立,
故选:B.
点评 本题考查了基本不等式的性质的应用,熟练掌握满足基本不等式的条件是解答本题的关键,本题是一道基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{127}{2}$ | B. | $\frac{255}{2}$ | C. | 64 | D. | 128 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
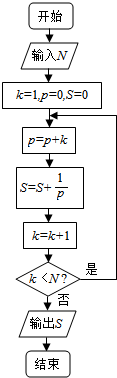
| A. | $\frac{7}{4}$ | B. | $\frac{8}{5}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 不含60°的等腰三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com