
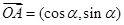 (
(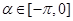 ),向量
),向量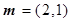 ,
,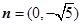 ,
,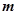
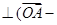
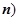 .
.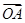 ; (Ⅱ)若
; (Ⅱ)若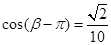 ,
,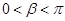 ,求
,求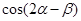 .
.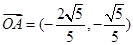 ……………6分
……………6分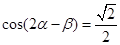 .
.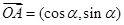 ,∴
,∴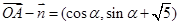 ,…………………1分
,…………………1分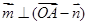 ,得到三角关系是
,得到三角关系是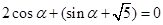 ,结合
,结合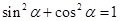 ,解得。
,解得。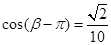 ,解得
,解得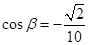 ,
,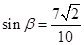 ,结合二倍角公式
,结合二倍角公式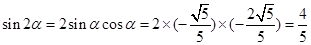 ,和
,和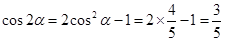 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。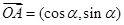 ,∴
,∴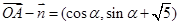 ,…………1分
,…………1分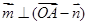 ,∴
,∴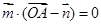 ,即
,即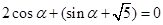 ① …………2分
① …………2分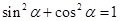 ② 由①②联立方程解得,
② 由①②联立方程解得,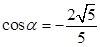 ,
,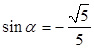 5分
5分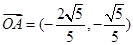 ……………6分
……………6分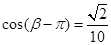 即
即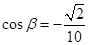 ,
,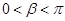 , …………7分
, …………7分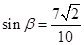 ,
,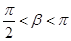 ………8分
………8分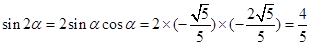 , ………9分
, ………9分 , ……10分
, ……10分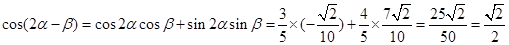 .
.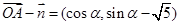 ,…………………………………1分
,…………………………………1分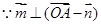 ,∴
,∴ ,即
,即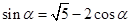 ,①……2分
,①……2分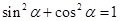 ②
②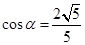 ③ …………………4分
③ …………………4分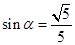 ……………………………………5分
……………………………………5分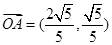 …………………………………6分
…………………………………6分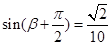 ,
,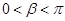 ,∴
,∴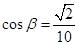 ,且
,且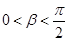 ……7分
……7分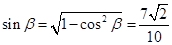 ,从而
,从而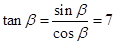 . …………………8分
. …………………8分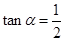 ,
, 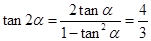 ; ………………9分
; ………………9分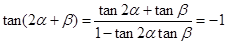 . ………………………………10分
. ………………………………10分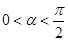 ,∴
,∴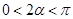 , 又
, 又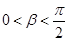 ,∴
,∴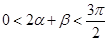 ……11分
……11分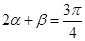 ………………………………12分
………………………………12分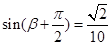 ,
,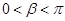 ,∴
,∴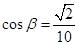 ,且
,且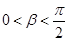 …………7分
…………7分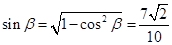 . ……………8分
. ……………8分 ,
,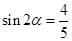 . …………9分
. …………9分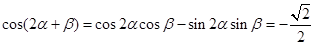 ……………10分
……………10分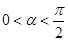 ,且注意到
,且注意到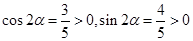 ,
,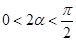 ,又
,又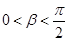 ,∴
,∴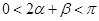 ………………………11分
………………………11分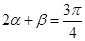 …………………12分
…………………12分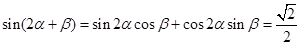 ,又∵
,又∵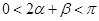 ∴
∴ 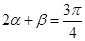 ,
,

科目:高中数学 来源:不详 题型:解答题

 ,
, ).
). |=|
|=| |,求角α的值;
|,求角α的值; ·
· =-1,求
=-1,求 的值.
的值.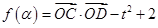 在定义域α∈(
在定义域α∈( ,
, )有最小值
)有最小值 ,求
,求 的值。
的值。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com