练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，是圆柱的直径，是圆柱的母线，，，点是圆柱底面圆周上的点.

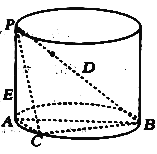
    （1）求三棱锥体积的最大值；

    （2）若，是线段上靠近点的三等分点，点是线段上的动点，求的最小值.

    【答案】（1）；（2）4

    【解析】

    （1）三棱锥的高为定值，要根据三棱锥体积公式可知，要使得体积最大，就要底面积最大，又因为边为定值，故当到的距离取得最大值时，底面积最大，故此时棱锥的体积最大；

    （2）反向延长至，使得三点共线，三点共线时，距离最短，则为最小值.

    （1）三棱锥高，，点到的最大值为底面圆的半径，

    则三棱锥体积的最大值等于.

    （2）将绕着旋转到使其共面，且在的反向延长线上，连接，与的交点为，此时最小，为；

    由，，且易知，由勾股定理知，因为，所以，则，；

    ，则是边长为4的等边三角形，故，所以的最小值等于4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若，用“五点法”在给定的坐标系中，画出函数在上的图象；

    （2）若为奇函数，求；

    （3）在（2）的前提下，将函数的图象向左平移个单位后，再将得到的图象上各点的横坐标伸长为原来的2倍，纵坐标不变，得到函数的图象，求在上的单调递增区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】科学家发现某种特别物质的温度（单位：摄氏度）随时间（时间：分钟）的变化规律满足关系式：（，）.

    （1）若，求经过多少分钟，该物质的温度为5摄氏度；

    （2）如果该物质温度总不低于2摄氏度，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，平面，正方形的边长为2，，设为侧棱的中点.

    （1）求正四棱锥的体积；

    （2）求直线与平面所成角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点在双曲线（，）上，且双曲线的一条渐近线的方程是．

    （1）求双曲线的方程；

    （2）若过点且斜率为的直线与双曲线有两个不同的交点，求实数的取值范围；

    （3）设（2）中直线与双曲线交于两个不同的点，若以线段为直径的圆经过坐标原点，求实数的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，其中，为个互不相同的有限集合，满足对任意、，均有.若（表示有限集合的元素个数），证明：存在，使得属于中的至少个集合.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知、为平面上的两个定点，且，该平面上的动线段的端点、，满足，，，则动线段所形成图形的面积为（ ）

    A.36B.60C.72D.108

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex﹣axlnx．

    （1）当a=1时，求曲线f（x）在x=1处的切线方程；

    （2）证明：对于a∈（0，e），函数f（x）在区间（）上单调递增．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年8月8日是我国第十个全民健身日，其主题是：新时代全民健身动起来。某市为了解全民健身情况，随机从某小区居民中抽取了40人，将他们的年龄分成7段：[10，20），[20，30），[30，40），[40，50），[50，60），[60，70），[70，80]后得到如图所示的频率分布直方图。

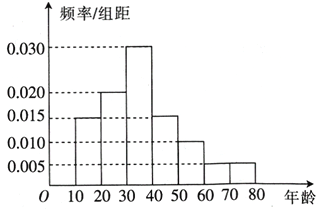
    （1）试求这40人年龄的平均数、中位数的估计值；

    （2）（i）若从样本中年龄在[50，70）的居民中任取2人赠送健身卡，求这2人中至少有1人年龄不低于60岁的概率；

    （ⅱ）已知该小区年龄在[10，80]内的总人数为2000，若18岁以上（含18岁）为成年人，试估计该小区年龄不超过80岁的成年人人数。

    查看答案和解析>>

    同步练习册答案