解:(I)∵P=(-∞,0),∴f(P)={y|y=|x|,x∈(-∞,0)}=(0,+∞),
∵M=[0,4],∴f(M)={y|y=-x
2+2x,x∈[0,4]}=[-8,1].
∴f(P)∪f(M)=[-8,+∞)
(II)若-3∈M,则f(-3)=-15∉[-3,2a-3],不符合要求
∴-3∈P,从而f(-3)=3
∵f(-3)=3∈[-3,2a-3]
∴2a-3≥3,得a≥3
若a>3,则2a-3>3>-(x-1)
2+1=-x
2+2x
∵P∩M=∅,∴2a-3的原象x
0∈P且3<x
0≤a
∴x
0=2a-3≤a,得a≤3,与前提矛盾
∴a=3
此时可取P=[-3,-1)∪[0,3],M=[-1,0),满足题意
(III)∵f(x)是单调递增函数,∴对任意x<0,有f(x)<f(0)=0,∴x∈M
∴(-∞,0)⊆M,同理可证:(1,+∞)⊆P
若存在0<x
0<1,使得x
0∈M,则1>f(x
0)=-

+2x
0>x
0,
于是[x
0,-

+2x
0]⊆M
记x
1=-

+2x
0∈(0,1),x
2=-

+2x
1,…
∴[x
0,x
1]∈M,同理可知[x
1,x
2]∈M,…
由x
n+1=-
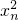
+2x
n,得1-x
n+1=1+
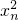
-2x
n=(1-
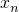
)
2;
∴1-x
n=(1-
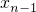
)
2=(1-x
n-2)2
2=…=(1-x
0)2
n对于任意x∈[x
0,1],取[log
2log
(1-x
0)(1-x)-1,log
2log
(1-x
0)(1-x)]中的自然数n
x,则
x∈[xn
x,xn
x+1]⊆M
∴[x
0,1)⊆M
综上所述,满足要求的P,M必有如下表示:
P=(0,t)∪[1,+∞),M=(-∞,0]∪[t,1),其中0<t<1
或者P=(0,t]∪[1,+∞),M=(-∞,0]∪(t,1),其中0<t<1
或者P=[1,+∞),M=(-∞,1]
或者P=(0,+∞),M=(-∞,0]
分析:(I)利用y=|x|的图象和性质和二次函数的图象和性质分别计算此分段函数两支上的值域,再求其并集即可;(II)抓住线索-3∈P∪M,逐层深入,先判断-3∈P,得a的范围,再由已知推理缩小此范围,最后确定a的值;(III)现根据函数的单调性确定∴(-∞,0)⊆M,(1,+∞)⊆P,再证明在(0,1)上存在分界点的话,这个分界点应具有怎样的性质,最后根据此性质写出满足题意的集合P,M
点评:本题综合考查了集合的表示方法和意义,函数的值域,逻辑推理和论证的能力,分析问题解决问题的能力

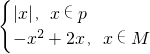 其中P,M是非空数集,且P∩M=φ,设f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
其中P,M是非空数集,且P∩M=φ,设f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}. +2x0>x0,
+2x0>x0, +2x0]⊆M
+2x0]⊆M +2x0∈(0,1),x2=-
+2x0∈(0,1),x2=- +2x1,…
+2x1,…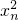 +2xn,得1-xn+1=1+
+2xn,得1-xn+1=1+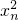 -2xn=(1-
-2xn=(1-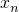 )2;
)2;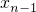 )2=(1-xn-2)22=…=(1-x0)2n
)2=(1-xn-2)22=…=(1-x0)2n
