解:(Ⅰ)由x
2-x+1≤2x-1,即x
2-3x+2≤0,解得:1≤x≤2,此时f(x)=x
2-x+1;
由x
2-x+1>2x-1,即x
2-3x+2>0,解得:x<1或x>2.
∴
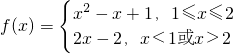
.
∴
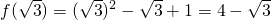
.
(Ⅱ)当1≤x≤2时,f(x)=x
2-x+1,
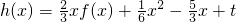
=
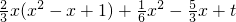
=
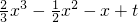
.
令
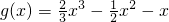
,
则函数h(x)的零点个数,即为函数y=g(x)与函数y=-t的交点个数.
由g
′(x)=2x
2-x-1=(2x+1)(x-1).
当x∈(1,2)时,g
′(x)>0,∴g(x)在(1,2)上单调递增.
又
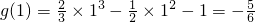
,
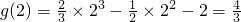
.
∴当
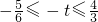
,即
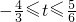
时,函数h(x)有一个零点;
当
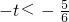
或
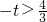
,即
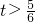
或
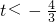
时,函数h(x)没有零点.
综上所述,当
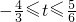
时,函数h(x)有一个零点;
当
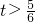
或
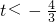
时,函数h(x)没有零点.
分析:(Ⅰ)通过求解不等式得到x
2-x+1≤2x-1和x
2-x+1>2x-1的x的取值范围,从而写出分段函数f(x),直接代入后可求f(

)的值;
(Ⅱ)求函数h(x)=
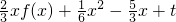
(t∈R)的零点个数,即求函数
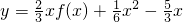
与函数y=x的交点个数,把函数f(x)的解析式代入后利用导数分析函数
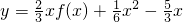
的极值点的情况,根据函数极值点的情况可得函数
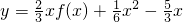
与函数y=x的交点个数,从而得到函数h(x)=
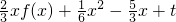
(t∈R)的零点个数.
点评:本题考查了利用导数研究函数的极值,考查了函数零点个数的判断,一个函数零点的个数,就是该函数对应的方程的根的个数,此类问题往往转化为另外两个函数交点的个数来解决,是中档题.

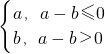 设函数f(x)=(x2-x+1)?(2x-1),其中x∈R
设函数f(x)=(x2-x+1)?(2x-1),其中x∈R )的值;
)的值;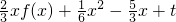 (t∈R)的零点个数.
(t∈R)的零点个数.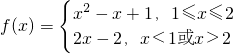 .
.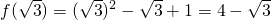 .
.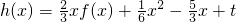 =
=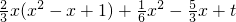 =
=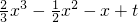 .
.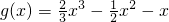 ,
,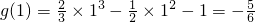 ,
,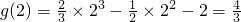 .
.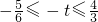 ,即
,即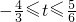 时,函数h(x)有一个零点;
时,函数h(x)有一个零点;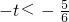 或
或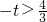 ,即
,即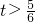 或
或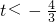 时,函数h(x)没有零点.
时,函数h(x)没有零点.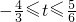 时,函数h(x)有一个零点;
时,函数h(x)有一个零点;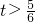 或
或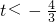 时,函数h(x)没有零点.
时,函数h(x)没有零点. )的值;
)的值;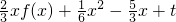 (t∈R)的零点个数,即求函数
(t∈R)的零点个数,即求函数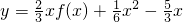 与函数y=x的交点个数,把函数f(x)的解析式代入后利用导数分析函数
与函数y=x的交点个数,把函数f(x)的解析式代入后利用导数分析函数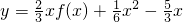 的极值点的情况,根据函数极值点的情况可得函数
的极值点的情况,根据函数极值点的情况可得函数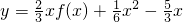 与函数y=x的交点个数,从而得到函数h(x)=
与函数y=x的交点个数,从而得到函数h(x)=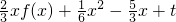 (t∈R)的零点个数.
(t∈R)的零点个数.
