
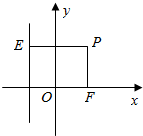
 ��ͼ����O������ԭ�㣬��F��p��0��������p��0����E��ֱ��l��x=-p�ϣ���F��ֱ��x+y=0�ľ������$\sqrt{2}$������p����|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|��$\overrightarrow{EP}$=��$\overrightarrow{OF}$���ˡ�R���Ҧˡ�0����
��ͼ����O������ԭ�㣬��F��p��0��������p��0����E��ֱ��l��x=-p�ϣ���F��ֱ��x+y=0�ľ������$\sqrt{2}$������p����|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|��$\overrightarrow{EP}$=��$\overrightarrow{OF}$���ˡ�R���Ҧˡ�0�������� ��1�������F�������������ߵĶ��壬����P�Ĺ켣M�ķ��̣�
��2��ֱ��m��y=x+b��켣M�����ɵ�y2-4y+4b=0�������ABD��������û�������ʽ������ֵ�����ɵó����ۣ�
��� �⣺��1���ߵ�F��p��0������ֱ��x+y=0�ľ������$\sqrt{2}$��
��$\frac{|p|}{\sqrt{2}}$=$\sqrt{2}$��
��p��0��
��p=2��
��F��2��0����
�߶���P����|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|��$\overrightarrow{EP}$=��$\overrightarrow{OF}$��
�ද��P�Ĺ켣M�ķ���Ϊy2=4x��
��2��ֱ��m��y=x+b��켣M�����ɵ�y2-4y+4b=0��
��y=2��2$\sqrt{1-b}$��
��K��-b��0����
���ABD���S=$\frac{1}{2}•��10+b��•4\sqrt{1-b}$=2$\sqrt{\frac{1}{2}��10+b����10+b����2-2b��}$��
�ߣ�10+b����10+b����2-2b����$��\frac{10+b+10+b+2-2b}{3}��^{3}$=$\frac{2{2}^{3}}{27}$��
��S��2$\sqrt{\frac{1}{2}•\frac{2{2}^{3}}{27}}$=$\frac{44}{9}\sqrt{33}$��
���ҽ���b=-$\frac{8}{3}$ʱ����ABD��������ֵΪ$\frac{44}{9}\sqrt{33}$��
���� ���⿼��켣���̣����������ߵĶ��壬��������������ļ��㣬�����������ʽ�����ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
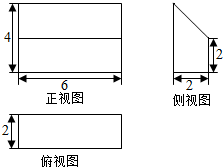
| A�� | 9 | B�� | 10 | C�� | 36 | D�� | 72 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | 1�Ź�� | 2�Ź�� | 3�Ź�� | 4�Ź�� |
| ������ | 20 | 30 | 40 | 10 |
| ʱ��t������/�ˣ� | 2 | 3 | 4 | 6 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com