
 平面PAD;
平面PAD;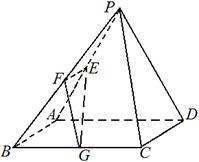
 I)证明:∵平面PAD⊥平面ABCD,
I)证明:∵平面PAD⊥平面ABCD, ,
,
 平面PAD, )
平面PAD, ) 平面PAD; …………4分
平面PAD; …………4分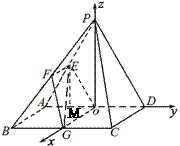 ∵
∵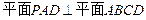 ,则PO
,则PO  平面ABCD.
平面ABCD.  平面ABCD.且OG
平面ABCD.且OG AO,
AO, EO ∴
EO ∴ 即为所求 …………8分
即为所求 …………8分 ,EM=
,EM= OM=1
OM=1  =
= 故
故  =
=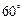
 锐二面角的大小是
锐二面角的大小是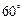 …………12分
…………12分 AD于O,∵
AD于O,∵ ,
,  平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系, …………2分
平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系, …………2分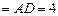 ,∴
,∴ ,
, ,
, , …………(4分)
, …………(4分) ,
, ,
, 平面PAD; …………4分
平面PAD; …………4分 ,
,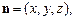
 ,
,  , …………8分
, …………8分 ……(12分)
……(12分) ,锐二面角的大小是
,锐二面角的大小是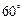 ; …………12分
; …………12分

科目:高中数学 来源:不详 题型:解答题
 F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;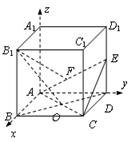
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
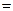 a,AD
a,AD 2,SA
2,SA 1,且SA⊥底面ABCD,若
1,且SA⊥底面ABCD,若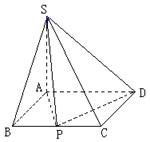
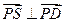 .
. 个单位法向量
个单位法向量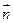
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
|
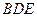 ?若存在,确定点N的位置;
?若存在,确定点N的位置; 若不存在,请说明理由.
若不存在,请说明理由. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A. 720 | B.900 | C. 1080  | D.1800 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com