
若函数 f(x)=ax (a>0,a≠1 ) 的部分对应值如表:
则不等 式f-1(│x│<0)的解集是
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
若函数 f(x)=a x (a>0,a≠1 ) 的部分对应值如表:
| x | -2 | 0 |
| f(x) | 0.592 | 1 |
则不等 式f-1(│x│<0)的解集是 ()
A. {x│-1<x<1} B. {x│x<-1或x>1}
C. {x│0<x<1} D. {x│-1<x<0或0<x<1}
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省商丘市高三5月第三次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数f (x)=lnx.
(Ⅰ)函数g(x)=3x-2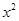 ,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
(Ⅱ)函数h(x)=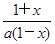 ,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
G(x)<-2,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届北京市高一上学期期中考试数学 题型:选择题
若函数f(x)=x+x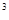 , x
, x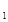 ,x
,x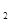
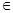 R,且x
R,且x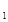 +x
+x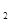 >0,则f(x
>0,则f(x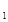 )+f(x
)+f(x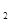 )的值
)的值
A、一定大于0 B、一定小于0 C、一定等于0 D、正负都有可能
查看答案和解析>>
科目:高中数学 来源:2014届北京市高一上学期期中考试数学 题型:选择题
若函数f(x)=3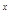 +3
+3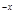 与g(x)=3
与g(x)=3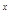 -3
-3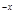 的定义域均为R,则
的定义域均为R,则
A、f(x)与g(x)均为偶函数
B、f(x)为偶函数,g(x)为奇函数
C、f(x)与g(x)均为奇函数
D、 f(x)为奇函数,g(x)为偶函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com