
【题目】已知y=f(x)是定义在R上的奇函数,且 ![]() 为偶函数,对于函数y=f(x)有下列几种描述,其中描述正确的是( ) ①y=f(x)是周期函数;②x=π是它的一条对称轴
为偶函数,对于函数y=f(x)有下列几种描述,其中描述正确的是( ) ①y=f(x)是周期函数;②x=π是它的一条对称轴
③(﹣π,0)是它图象的一个对称中心;④当 ![]() 时,它一定取最大值
时,它一定取最大值
A.①②
B.①③
C.②④
D.②③
【答案】B
【解析】解答:由已知可得:f(﹣x)=﹣f(x) …(1)
f(﹣x﹣ ![]() )=﹣f(x+
)=﹣f(x+ ![]() )…(2)
)…(2)
f(﹣x+ ![]() )=f(x+
)=f(x+ ![]() )…(3)
)…(3)
由(3)知 函数f(x)有对称轴x= ![]()
由(2)(3)得 f(﹣x﹣ ![]() )=﹣f(﹣x+
)=﹣f(﹣x+ ![]() );
);
令z=﹣x+ ![]() 则﹣x﹣
则﹣x﹣ ![]() =z﹣π,
=z﹣π,
∴f(z﹣π)=﹣f(z),
故有f(z﹣π﹣π)=﹣f(z﹣π),
两者联立得 f(z﹣2π)=f(z),
可见函数f(x)是周期函数,且周期为2π;
由(1)知:f(﹣z)=﹣f(z),代入上式得:f(z﹣2π)=﹣f(﹣z);
由此式可知:函数f(x)有对称中心(﹣π,0)
由上证知①③是正确的命题.
故应选B
分析:本题函数的性质,先对已知y=f(x)是定义在R上的奇函数,且 ![]() 为偶函数用定义转化为恒等式,再由两个恒等式进行合理变形得出与四个命题有关的结论,通过推理证得①③正确.
为偶函数用定义转化为恒等式,再由两个恒等式进行合理变形得出与四个命题有关的结论,通过推理证得①③正确.
【考点精析】认真审题,首先需要了解函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇).


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】将5个小球放到3个盒子中,在下列条件下,各有多少种投放方法?
①小球不同,盒子不同,盒子不空;
②小球不同,盒子不同,盒子可空;
③小球不同,盒子相同,盒子不空;
④小球不同,盒子相同,盒子可空;
⑤小球相同,盒子不同,盒子不空;
⑥小球相同,盒子不同,盒子可空;
⑦小球相同,盒子相同,盒子不空;
⑧小球相同,盒子相同.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为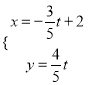 (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,
, ![]() 是直线
是直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(Ⅱ)若直线![]() 被圆
被圆![]() 截得的弦长等于圆
截得的弦长等于圆![]() 的半径
的半径![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为实数集R,集合A={x|y= ![]() +
+ ![]() },B={x|log2x>1}.
},B={x|log2x>1}.
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校要从参加数学竞赛的1000名学生中,随机抽取50名学生的成绩进行分析,现将参加数学竞赛的1000名学生编号如下000,001,002,…,999,如果在第一组随机抽取的一个号码为015,则抽取的第40个号码为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com