
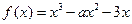
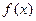 在
在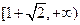 是增函数,导函数
是增函数,导函数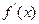 在
在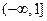 上是减函数,求
上是减函数,求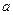 的值;
的值;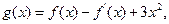 求
求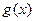 的单调区间.
的单调区间. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
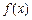 的定义域为R,其导数
的定义域为R,其导数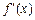 满足0<
满足0<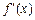 <1.设a是方程
<1.设a是方程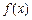 =x的根.
=x的根.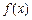 <x;
<x;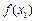 -
-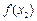 |<|x1-x2|(x1,x2∈R,x1≠x2);
|<|x1-x2|(x1,x2∈R,x1≠x2);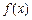 ,满足0<
,满足0<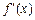 <1,且
<1,且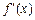 不为常数.
不为常数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值
万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值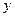 万元与技术改造投入
万元与技术改造投入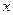 万元之间的关系满足:①
万元之间的关系满足:①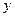 与
与 和
和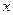 的乘积成正比;②
的乘积成正比;②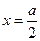 时,
时, ;③
;③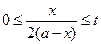 ,其中
,其中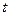 为常数,且
为常数,且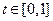 。
。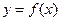 ,求
,求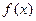 表达式,并求
表达式,并求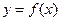 的定义域;
的定义域;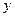 的最大值,并求出此时的技术改造投入。
的最大值,并求出此时的技术改造投入。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.5m | B.3.5m | C.5.5m | D.7.5m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com