
【题目】下列说法中,正确的有_______.(写出所有正确说法的序号)
①在![]() 中,若
中,若![]() ,则
,则![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形;
是锐角三角形;
③在![]() 中,若
中,若![]() ,则
,则![]() ;
;
④若![]() 是等差数列,其前
是等差数列,其前![]() 项和为
项和为![]() ,则三点
,则三点![]()
![]()
![]() 共线;
共线;
⑤等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,点
,点![]() 均在函数
均在函数![]() (
(![]() 且
且![]() ,
,![]()
![]() 均为常数)的图象上,则
均为常数)的图象上,则![]() 的值为
的值为![]() .
.
【答案】①③④⑤
【解析】
根据正弦定理及边角关系可判断①;根据正弦定理及余弦定理,可判断角![]() 为锐角,但不能判断角
为锐角,但不能判断角![]() 和角
和角![]() 的情况,因而②错误;结合正弦定理及余弦定理可判断角
的情况,因而②错误;结合正弦定理及余弦定理可判断角![]() 为钝角,结合正切的和角公式,变形后即可判断③;根据等差数列前n项和的性质,结合两点间的斜率公式,可判断④;将点带入函数解析式,结合
为钝角,结合正切的和角公式,变形后即可判断③;根据等差数列前n项和的性质,结合两点间的斜率公式,可判断④;将点带入函数解析式,结合![]() 求得通项公式,结合等比数列的定义即可求得
求得通项公式,结合等比数列的定义即可求得![]() .
.
对于①,在![]() 中,若
中,若![]() ,则由大角对大边可知
,则由大角对大边可知![]() .设
.设![]() 外接圆半径为
外接圆半径为![]() ,由正弦定理可知
,由正弦定理可知![]() ,即
,即![]() .所以①正确;
.所以①正确;
对于②,在![]() 中,若
中,若![]() ,由正弦定理可得
,由正弦定理可得![]() ,可判定角
,可判定角![]() 为锐角.但当角
为锐角.但当角![]() 或角
或角![]() 为钝角时也成立,因而不能说明是锐角三角形,所以②错误.
为钝角时也成立,因而不能说明是锐角三角形,所以②错误.
对于③,在![]() 中,若
中,若![]() ,由正弦定理可知
,由正弦定理可知![]() ,则
,则![]() ,所以角
,所以角![]() 为钝角.由正切和角公式可知,
为钝角.由正切和角公式可知,![]() ,
,
所以![]()
![]()
![]()
所以![]()
因为角![]() 为钝角,所以角
为钝角,所以角![]() 和角
和角![]() 必为锐角,因而
必为锐角,因而![]() ,所以
,所以![]() ,所以③正确;
,所以③正确;
对于④,![]() 是等差数列,其前
是等差数列,其前![]() 项和为
项和为![]() ,则由等差数列前
,则由等差数列前![]() 项和公式可得
项和公式可得![]() ,则
,则![]() .所以
.所以![]() ,
,![]() ,
,![]()
由两点间斜率公式可得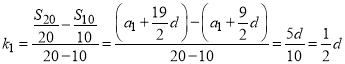
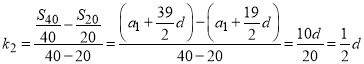
由![]() 可知三点共线,所以④正确;
可知三点共线,所以④正确;
对于⑤,点![]() 均在函数
均在函数![]() (
(![]() 且
且![]() ,
,![]()
![]() 均为常数)的图象上.
均为常数)的图象上.
则![]()
所以当![]() 时,
时,![]()
当![]() 时,
时,![]()
因为![]() 为等比数列,则首项也满足通项公式,所以
为等比数列,则首项也满足通项公式,所以![]()
解得![]() ,所以⑤正确.
,所以⑤正确.
综上可知,正确的为①③④⑤
故答案为: ①③④⑤


科目:高中数学 来源: 题型:
【题目】有10所学校,每所都选派若干名男生和若干名女生举行跳棋比赛,同一学校的选手不比赛,不同学校的选手不论男女在两人之间都要进行一场比赛. 在两个男生或两个女生之间的比赛总局数与男生和女生之间的比赛总局数与男生和女生之间的比赛总局数至多相差1,而男生的总人数和女生的总人数也至多相差1. 求证:至少有7所学校选派的男生和女生人数相同.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知n为给定的正整数,t为给定的实数,设(t+x)n=a0+a1x+a2x2+…+anxn.
(1)当n=8时.
①若t=1,求a0+a2+a4+a6+a8的值;
②若t=![]() ,求数列{an}中的最大值;
,求数列{an}中的最大值;
(2)若t=![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.若![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题
均为假命题
D.命题![]() :“
:“![]() ,使得
,使得![]() ”,则非
”,则非![]() :“
:“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 为固定的整数,定义任意整数坐标点
为固定的整数,定义任意整数坐标点![]() 关于
关于![]() 的余数是
的余数是![]() 关于
关于![]() 的余数.找出所有正整数数组
的余数.找出所有正整数数组![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的长方形具有如下性质:
为顶点的长方形具有如下性质:
ⅰ.长方形内整数点以![]() 为余数出现的次数相同;
为余数出现的次数相同;
ⅱ.长方形边界上整数点以![]() 为余数出现的次数相同.
为余数出现的次数相同.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一湖中有不在同一直线的三个小岛A、B、C,前期为开发旅游资源在A、B、C三岛之间已经建有索道供游客观赏,经测量可知AB两岛之间距离为3公里,BC两岛之间距离为5公里,AC两岛之间距离为7公里,现调查后发现,游客对在同一圆周上三岛A、B、C且位于![]() (优弧)一片的风景更加喜欢,但由于环保、安全等其他原因,没办法尽可能一次游览更大面积的湖面风光,现决定在
(优弧)一片的风景更加喜欢,但由于环保、安全等其他原因,没办法尽可能一次游览更大面积的湖面风光,现决定在![]() 上选择一个点D建立索道供游客游览,经研究论证为使得游览面积最大,只需使得△ADC面积最大即可.则当△ADC面积最大时建立索道AD的长为______公里.(注:索道两端之间的长度视为线段)
上选择一个点D建立索道供游客游览,经研究论证为使得游览面积最大,只需使得△ADC面积最大即可.则当△ADC面积最大时建立索道AD的长为______公里.(注:索道两端之间的长度视为线段)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方形花圃被分成5份.
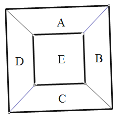
(1)若给这5个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿4种颜色不同的花,求有多少种不同的种植方法?
(2)若将6个不同的盆栽都摆放入这5个部分,且要求每个部分至少有一个盆栽,问有多少种不同的放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com