
【题目】如图,在几何体![]() 中,四边形
中,四边形![]() 为直角梯形,
为直角梯形, ![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的大小.
所成的锐二面角的大小.
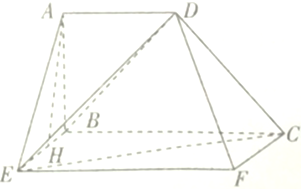
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,易证得四边形
,易证得四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,进而得证;
,进而得证;
(2)先证得![]() ,
, ![]() ,
, ![]() 两两垂直,以点
两两垂直,以点![]() 为原点,以
为原点,以![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标系,利用平面
轴,建立空间直角坐标系,利用平面![]() 与平面
与平面![]() 的法向量求解即可.
的法向量求解即可.
试题解析:
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
,
∵![]() 为
为![]() 中点,∴
中点,∴![]() ,且
,且![]() .
.
∵四边形![]() 为直角梯形,
为直角梯形, ![]() ,且
,且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
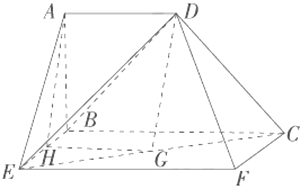
(2)因为四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
,
所以![]() ,∴
,∴![]() .
.
又![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
所以![]() ,因此
,因此![]() .
.
以点![]() 为原点,以
为原点,以![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则有 令
令![]() ,则
,则![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
, ![]() ,
, ![]() ,
,
则有 令
令![]() ,则
,则![]() ,
,
所以![]() ,
,
所以平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.



科目:高中数学 来源: 题型:
【题目】设函数![]() ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )
①当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;②当
上有最小值;②当![]() 时,函数
时,函数![]() 在
在![]() 是单调增函数;③若
是单调增函数;③若![]() ,则
,则![]() ;④方程
;④方程![]() 可能有三个实数根.
可能有三个实数根.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )

A. 平面ABD⊥平面ABC B. 平面ADC⊥平面BDC
C. 平面ABC⊥平面BDC D. 平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等腰梯形ABCD(如图1所示),其中AB∥CD,E,F分别为AB和CD的中点,且AB=EF=2,CD=6,M为BC中点.现将梯形ABCD沿着EF所在直线折起,使平面EFCB⊥平面EFDA(如图2所示),N是线段CD上一动点,且![]() .
.

(1)求证:MN∥平面EFDA;
(2)求三棱锥A-MNF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市上年度电价为0.80元/千瓦时,年用电量为![]() 千瓦时.本年度计划将电价降到0.55元/千瓦时~0.7元/千瓦时之间,而居民用户期望电价为0.40元/千瓦时(该市电力成本价为0.30元/千瓦时),经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为
千瓦时.本年度计划将电价降到0.55元/千瓦时~0.7元/千瓦时之间,而居民用户期望电价为0.40元/千瓦时(该市电力成本价为0.30元/千瓦时),经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为![]() .试问当地电价最低为多少元/千瓦时,可保证电力部门的收益比上年度至少增加20%.
.试问当地电价最低为多少元/千瓦时,可保证电力部门的收益比上年度至少增加20%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 (
(![]() 为参数),曲线
为参数),曲线 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立直角坐标系.
轴的正半轴为极轴建立直角坐标系.
(1)求曲线![]() 的极坐标方程,直线
的极坐标方程,直线![]() 的普通方程;
的普通方程;
(2)把直线![]() 向左平移一个单位得到直线
向左平移一个单位得到直线![]() ,设
,设![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,
, ![]() ,
, ![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com