
分析 (1)通过n=1,a1=S1=2,然后求解数列的Sn,利用新定义判断即可.
(2)求出Sn,对任意n∈N*,存在m∈N*使Sn=am,利用新定义判断即可.
(3)n≥2时,推出an+1=qan,求出${a_n}=\left\{\begin{array}{l}2t({n=1})\\ p•{q^{n-2}}({n≥2})\end{array}\right.$,通过q=1时,推出{an}不是“H数列”,q≠1时,求出Sn,利用新定义推出q=2,r=0,t>0的正实数.
解答 解:(1)n=1,a1=S1=2,
∴${S}_{n}=\frac{2(1-{2}^{n})}{1-2}$=2n+1-2(1分)
∴2n-1是奇数,2m-1是偶数;(2分)
∴2n+1-2≠2m(3分)
∴{an}不是“H数列”(4分)
(2)${S_n}=n{a_1}+\frac{n(n-1)}{2}d=2dn+\frac{n(n-1)}{2}d$(6分)
对任意n∈N*,存在m∈N*使Sn=am,即$n{a_1}+\frac{n(n-1)}{2}d={a_1}+(m-1)d$$m=2n-1+\frac{n(n-1)}{2}$(8分)
n,n-1是一奇一偶,∴m一定是自然数;(10分)
(3)n≥2时(1-q)Sn+an+1=r,(1-q)Sn-1+an=r(1-q)an+an+1-an=0,
∴an+1=qan(12分)
(1-q)×2t+a2=ra2=r+2qt-2t=p,(13分)
∴${a_n}=\left\{\begin{array}{l}2t({n=1})\\ p•{q^{n-2}}({n≥2})\end{array}\right.$.(14分)
q=1时,${a_n}=\left\{\begin{array}{l}2t({n=1})\\ r({n≥2})\end{array}\right.$,Sn=2t+(n-1)r=r不恒成立 显然{an}不是“H数列”,(15分)
q≠1时${S_n}=2t+\frac{{p({1-{q^{n-1}}})}}{1-q}=2t+\frac{p}{1-q}-\frac{{p{q^{n-1}}}}{1-q}$,(16分)
n=1,S1=a1{an}是“H数列”,所以对任意n≥2时,存在m∈N*成立,
∴${S_n}=2t+\frac{p}{1-q}-\frac{{p{q^{n-1}}}}{1-q}=p{q^{m-2}}$,可得$-\frac{p{q}^{n-1}}{1-q}=p{q}^{m-2}$,即qn-1=(q-1)qm-2,解得q=2,
∴q=2,由$2t+\frac{p}{1-q}=0$,得p=2t,
由r+2qt-2t=p,∴r+4t-2t=2t,r=0,
∴q=2,r=0,t>0的正实数 (18分)
点评 本题考查数列的应用,数列与函数相结合,考查新定义的应用,转化思想以及分析问题解决问题的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
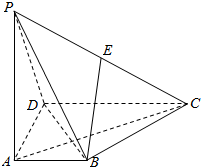 如图,在四棱锥P-ABCD中,PA⊥ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com