
【题目】在参加某次社会实践的学生中随机选取![]() 名学生的成绩作为样本,这
名学生的成绩作为样本,这![]() 名学生的成绩全部在
名学生的成绩全部在![]() 分至
分至![]() 分之间,现将成绩按如下方式分成
分之间,现将成绩按如下方式分成![]() 组:第一组,成绩大于等于
组:第一组,成绩大于等于![]() 分且小于
分且小于![]() 分;第二组,成绩大于等于
分;第二组,成绩大于等于![]() 分且小于
分且小于![]() 分;
分;![]() 第六组,成绩大于等于
第六组,成绩大于等于![]() 分且小于等于
分且小于等于![]() 分,据此绘制了如图所示的频率分布直方图.在选取的
分,据此绘制了如图所示的频率分布直方图.在选取的![]() 名学生中.
名学生中.
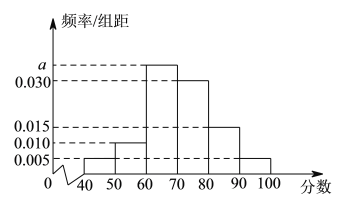
(Ⅰ)求![]() 的值及成绩在区间
的值及成绩在区间![]() 内的学生人数.
内的学生人数.
(Ⅱ)从成绩小于![]() 分的学生中随机选
分的学生中随机选![]() 名学生,求最多有
名学生,求最多有![]() 名学生成绩在区间
名学生成绩在区间![]() 内的概率.
内的概率.
科目:高中数学 来源: 题型:
【题目】设命题![]() :函数
:函数![]() 的定义域为
的定义域为![]() ;命题
;命题![]() :关于
:关于![]() 的方程
的方程![]() 有实根.
有实根.
(1)如果![]() 是真命题,求实数
是真命题,求实数![]() 的取值范围.
的取值范围.
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱![]() 容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面
容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面![]() 水平放置,如图所示,点
水平放置,如图所示,点![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在棱
分别在棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 上,水面恰好过点
上,水面恰好过点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() .
.

(1)证明: ![]() ;
;
(2)若底面![]() 水平放置时,求水面的高.
水平放置时,求水面的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别是
的两个焦点分别是![]() ,
, ![]() ,且点
,且点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于异于
相交于异于![]() 的不同两点
的不同两点![]() ,
, ![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有![]() 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,求取出的两个球编号之和为
次,求取出的两个球编号之和为![]() 的概率.
的概率.
(Ⅱ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,求恰有
次,求恰有![]() 次抽到
次抽到![]() 号球的概率.
号球的概率.
(Ⅲ)若一次从袋中随机抽取![]() 个球,记球的最大编号为
个球,记球的最大编号为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
(Ⅳ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,记球的最大编号为
次,记球的最大编号为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在游学活动中,在![]() 处参观的第
处参观的第![]() 组同学通知在
组同学通知在![]() 处参观的第
处参观的第![]() 组同学:第
组同学:第![]() 组正离开
组正离开![]() 处向
处向![]() 的东南方向游玩,速度约为
的东南方向游玩,速度约为![]() 米/分钟.已知
米/分钟.已知![]() 在
在![]() 的南偏西
的南偏西![]() 方向且相距
方向且相距![]() 米,第
米,第![]() 组同学立即出发沿直线行进并用
组同学立即出发沿直线行进并用![]() 分钟与第
分钟与第![]() 组同学汇合.
组同学汇合.
(![]() )设第
)设第![]() 组同学行进的方位角为
组同学行进的方位角为![]() ,求
,求![]() .
.
(方位角:从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)
(![]() )求第
)求第![]() 组同学的行进速度为多少?
组同学的行进速度为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,曲线
,曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() ;曲线
;曲线![]() 上的点
上的点![]() 在
在![]() 轴的右边且
轴的右边且![]() 到
到![]() 的距离与它到
的距离与它到![]() 轴的距离的差为1.
轴的距离的差为1.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,直线
,直线![]() 分别与
分别与![]() 相交于点
相交于点![]() 和
和![]() .求
.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com