
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 为椭圆上一点(在
为椭圆上一点(在![]() 轴上方),连结
轴上方),连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]() .
.

(1)若点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的周长为8,求椭圆
的周长为8,求椭圆![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 轴,且椭圆
轴,且椭圆![]() 的离心率
的离心率![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)[
(2)[![]() ,5].
,5].
【解析】
试题分析:(1)根据椭圆定义,将三角形周长转化为:4a=8,再结合点P在椭圆上,得![]() ,解方程组得a=2,b2=3.(2)由于
,解方程组得a=2,b2=3.(2)由于![]() 垂直于
垂直于![]() 轴,所以P(c,
轴,所以P(c,![]() ).再根据
).再根据![]() ,可求得Q(-
,可求得Q(-![]() c,-
c,-![]() ).代入椭圆方程得
).代入椭圆方程得![]() +
+![]() =1,即λ=
=1,即λ=![]() ,最后根据
,最后根据![]() ,确定实数
,确定实数![]() 的取值范围.
的取值范围.
试题解析:(1)因为F1,F2为椭圆C的两焦点,且P,Q为椭圆上的点,
所以PF1+PF2=QF1+QF2=2a,从而△PQF2的周长为4a.
由题意,得4a=8,解得a=2.
因为点P的坐标为 (1,![]() ),所以
),所以![]() ,
,
解得b2=3.
所以椭圆C的方程为![]() .
.
(2)方法一:因为PF2⊥x轴,且P在x轴上方,故设P(c,y0),y0>0.设Q(x1,y1).
因为P在椭圆上,所以![]() ,解得y0=
,解得y0=![]() ,即P(c,
,即P(c,![]() ).
).
因为F1(-c,0),所以![]() =(-2c,-
=(-2c,-![]() ),
),![]() =(x1+c,y1).
=(x1+c,y1).
由![]() =λ
=λ![]() ,得-2c=λ(x1+c),-
,得-2c=λ(x1+c),-![]() =λy1,
=λy1,
解得x1=-![]() c,y1=-
c,y1=-![]() ,所以Q(-
,所以Q(-![]() c,-
c,-![]() ).
).
因为点Q在椭圆上,所以(![]() )2e2+
)2e2+![]() =1,
=1,
即(λ+2)2e2+(1-e2)=λ2,(λ2+4λ+3)e2=λ2-1,
因为λ+1≠0,
所以(λ+3)e2=λ-1,从而λ=![]() .
.
因为e∈[![]() ,
,![]() ],所以
],所以![]() ≤e2≤
≤e2≤![]() ,即
,即![]() ≤λ≤5.
≤λ≤5.
所以λ的取值范围为[![]() ,5].
,5].
方法二:因为PF2⊥x轴,且P在x轴上方,故设P(c,y0),y0>0.
因为P在椭圆上,所以![]() +
+![]() =1,解得y0=
=1,解得y0=![]() ,即P(c,
,即P(c,![]() ).
).
因为F1(-c,0),故直线PF1的方程为y=![]() (x+c).
(x+c).
由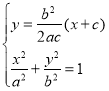 ,得(4c2+b2)x2+2b2cx+c2(b2-4a2)=0.
,得(4c2+b2)x2+2b2cx+c2(b2-4a2)=0.
因为直线PF1与椭圆有一个交点为P(c,![]() ).设Q(x1,y1),
).设Q(x1,y1),
则x1+c=-![]() ,即-c-x1=
,即-c-x1=![]() .
.
因为![]() =λ
=λ![]() ,
,
所以λ=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
因为e∈[![]() ,
,![]() ],所以
],所以![]() ≤e2≤
≤e2≤![]() ,即
,即![]() ≤λ≤5.
≤λ≤5.
所以λ的取值范围为[![]() ,5].
,5].


科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. ![]() ,
, ![]() 为不共线向量,若
为不共线向量,若![]() ,则
,则![]()
B. 若![]() ,
, ![]() 为平面内两个不相等向量,则平面内任意向量
为平面内两个不相等向量,则平面内任意向量![]() 都可以表示为
都可以表示为![]()
C. 若![]() ,
, ![]() ,则
,则![]() 与
与![]() 不一定共线
不一定共线
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
⑴从区间![]() 内任取一个实数
内任取一个实数![]() ,设事件
,设事件![]() 表示“函数
表示“函数![]() 在区间
在区间![]() 上有两个不同的零点”,求事件
上有两个不同的零点”,求事件![]() 发生的概率;
发生的概率;
⑵若联系掷两次一颗均匀的骰子(骰子六个面上标注的点数分别为![]() )得到的点数分别为
)得到的点数分别为![]() 和
和![]() ,记事件
,记事件![]() 表示“
表示“![]() 在
在![]() 上恒成立”,求事件
上恒成立”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于
的距离之比等于![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为
所截得的线段的长为![]() ,求直线
,求直线![]() 的方程
的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”活动. 为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
)进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
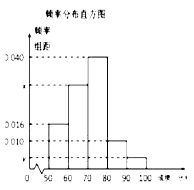

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设![]() 表示所抽取的3名同学中得分在[80,90)的学生人数,求
表示所抽取的3名同学中得分在[80,90)的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和点
和点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求定点![]() 的坐标;
的坐标;
(2)求圆![]() 的方程;
的方程;
(3)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点![]() ,问:在
,问:在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有__________.(写出所有正确说法的序号)
①已知关于![]() 的不等式
的不等式![]() 的角集为
的角集为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .
.
②已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 、
、![]() 、
、![]() 也构成等比数列.
也构成等比数列.
③已知函数 (其中
(其中![]() 且
且![]() )在
)在![]() 上单调递减,且关于
上单调递减,且关于![]() 的方程
的方程![]() 恰有两个不相等的实数解,则
恰有两个不相等的实数解,则![]() .
.
④已知![]() ,且
,且![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
⑤在平面直角坐标系中, ![]() 为坐标原点,
为坐标原点, ![]() 则
则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
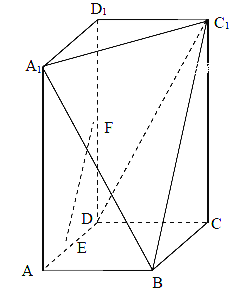
【题目】在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,过
,过![]() 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体![]() ,且这个几何体的体积为
,且这个几何体的体积为![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 的长;
的长;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与
与![]() 垂直,如果存在,求线段
垂直,如果存在,求线段![]() 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com