
【题目】某精密仪器生产有两道相互独立的先后工序,每道工序都要经过相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,两道工序都合格,产品才完全合格,.经长期监测发现,该仪器第一道工序检查合格的概率为 ![]() ,第二道工序检查合格的概率为
,第二道工序检查合格的概率为 ![]() ,已知该厂三个生产小组分别每月负责生产一台这种仪器.
,已知该厂三个生产小组分别每月负责生产一台这种仪器.
(1)求本月恰有两台仪器完全合格的概率;
(2)若生产一台仪器合格可盈利5万元,不合格则要亏损1万元,记该厂每月的赢利额为ξ,求ξ的分布列和每月的盈利期望.
【答案】
(1)解:设恰有两台仪器完全合格的事件为A,每台仪器经两道工序检验完全合格的概率为 ![]()
所以 ![]() …
…
(2)解:每月生产的仪器完全合格的台数可为3,2,1,0四种
所以赢利额ξ的数额可以为15,9,3,﹣3…(7分)
当ξ=15时, ![]()
当ξ=9时, ![]()
当ξ=3时, ![]()
当ξ=﹣3时, ![]()
每月的盈利期望 ![]()
所以每月的盈利期望值为10.14万元
【解析】(1)求出每生产一台合格仪器的概率,利用独立重复试验的概率公式求本月恰有两台仪器完全合格的概率;(2)根据题意得到变量的可能的取值,根据变量对应的事件,利用独立重复试验的概率公式得到概率,写出分布列,根据做出的变量的分布列,代入求期望值的公式做出期望值
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为![]() (
(![]() ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72![]() ,肚脐至足底长度为103
,肚脐至足底长度为103![]() ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从高三抽出![]() 名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
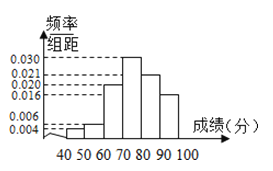
(1)这![]() 名学生成绩的众数与中位数;
名学生成绩的众数与中位数;
(2)这![]() 名学生的平均成绩.
名学生的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为![]() ,
,![]() ,
,![]() ,乙协会编号为
,乙协会编号为![]() ,丙协会编号分别为
,丙协会编号分别为![]() ,
,![]() ,若从这6名运动员中随机抽取2名参加双打比赛.
,若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP. 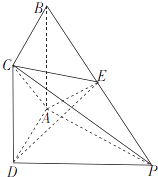
(1)证明:AC⊥DE;
(2)若PC= ![]() BC,求二面角E﹣AC﹣P的余弦值.
BC,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3﹣x2=2.(12分)
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)如图,在平面直角坐标系xOy中,依次连接点P1(x1 , 1),P2(x2 , 2)…Pn+1(xn+1 , n+1)得到折线P1 P2…Pn+1 , 求由该折线与直线y=0,x=x1 , x=xn+1所围成的区域的面积Tn . 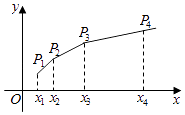
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com