分析:(I)证明CG⊥平面A1GC1,利用面面垂直的判定定理,即可证明平面A1CG⊥平面A1GC1;
(II)(法一)建立如图所示的空间坐标系,求出平面ABC与平面A1CG的法向量,利用向量的夹角公式,即可求得结论;
(法二)延长A1G、AB相交于P,过A作AF⊥PC交PC延长线于点F,连接A1F,证明∠AFA1为平行面ABC于平面A1CG所成二面角的平面角,即可得出结论.
解答: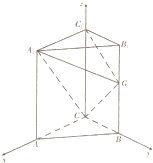
(I)证明:在直棱柱ABC-A
1B
1C
1中,有A
1C
1⊥CC
1.
∵∠ACB=90°,∴A
1C
1⊥C
1B
1,即A
1C
1⊥平面C
1CBB
1,
∵CG?平面C
1CBB
1,∴A
1C
1⊥CG.┉┉┉┉┉┉┉┉(2分)
在矩形C
1CBB
1中,CC
1=BB
1=2BC,G为BB
1的中点,
CG=
BC,C
1G=
BC,CC
1=2BC
∴∠CGC
1=90,即CG⊥C
1G┉┉┉┉┉┉┉┉(4分)
而A
1C
1∩C
1G=C
1,
∴CG⊥平面A
1GC
1.
∴平面A
1CG⊥平面A
1GC
1.┉┉┉┉┉┉┉┉(6分)
(II)解:(法一)由于CC
1平面ABC,∠ACB=90°,建立如图所示的空间坐标系,设AC=BC=
CC=a,则A(a,0,0),B(0,a,0)A
1(a,0,2a),G(0,a,a).
∴
=(a,0,2a),
=(0,a,a).┉┉┉┉┉┉┉┉(8分)
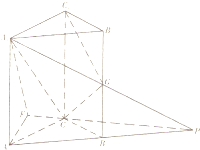
设平面A
1CG的法向量n
1=(x
1,y
1,z
1),
由
得
令z
1=1,n
1=(-2,-1,1).┉┉┉┉┉┉┉┉(9分)
又平面ABC的法向量为n
2=(0,0,1)┉┉┉┉┉┉┉┉(10分)
设平面ABC与平面A
1CG所成锐二面角的平面角为θ,
则
cosθ=||==┉┉┉┉┉┉┉┉(11分)
即平面ABC与平面A
1CG所成锐二面角的平面角的余弦值为
.┉┉┉(12分)
(法二)延长A
1G、AB相交于P,过A作AF⊥PC交PC延长线于点F,连接A
1F
∵AA
1⊥平面ABC,AF⊥PC,∴A
1F⊥PF
∴∠AFA
1为平面ABC与平面A
1CG所成二面角的平面角.┉┉┉┉┉┉┉┉(8分)
由(I)知CG⊥A
1G,∴△PGC~△PFA
1,
设AC=BC=a,∴
CG=a,A1G=GP=a,CP=a由
=,
得
A1F===┉┉┉┉┉┉┉┉┉┉(10分)
AF==a.
∴
cos∠AFA1===.┉┉┉┉┉(12分)
点评:本题考查面面垂直,考查面面角,考查向量知识的运用,考查学生的计算能力,属于中档题.

 (2009•临沂一模)如图,在直棱柱ABC-A1B1C1中,AC=BC=
(2009•临沂一模)如图,在直棱柱ABC-A1B1C1中,AC=BC= (I)证明:在直棱柱ABC-A1B1C1中,有A1C1⊥CC1.
(I)证明:在直棱柱ABC-A1B1C1中,有A1C1⊥CC1.


 字词句段篇系列答案
字词句段篇系列答案