练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数f（x）=ax2+bx+c（a≠0），对任意实数t都有f（2+t）=f（2﹣t）成立，则函数值f（﹣1），f（1），f（2），f（5）中，最小的一个不可能是（ ）
    A.f（﹣1）
    B.f（1）
    C.f（2）
    D.f（5）

    【答案】B
    【解析】解：∵对任意实数t都有f（2+t）=f（2﹣t）成立，
    ∴函数f（x）=ax2+bx+c（a≠0）的对称轴是x=2，
    当a＞0时，函数值f（﹣1），f（1），f（2），f（5）中，最小的一个是f（2）．
    当a＜0时，函数值f（﹣1），f（1），f（2），f（5）中，最小的一个是f（﹣1）和f（5）．
    故选B．
    【考点精析】掌握二次函数的性质是解答本题的根本，需要知道当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】（本小题共13分）

    以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊，无法确认，在图中经X表示。

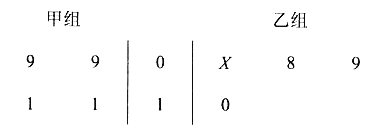
    （Ⅰ）如果X=8，求乙组同学植树棵数的平均数和方差；

    （Ⅱ）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率。

    （注：方差其中为，，的平均数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把函数f（x）= 图象上各点向右平移（＞0）个单位，得到函数g（x）=sin2x的图象，则的最小值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某冷饮店的经营状况，随机记录了该店月的月营业额（单位：万元）与月份的数据，如下表：

    （1）求关于的回归直线方程；

    （2）若在这些样本点中任取两点，求恰有一点在回归直线上的概率.

    附：回归直线方程中，

    ，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是出租汽车计价器的程序框图，其中表示乘车里程(单位：)，表示应支付的出租汽车费用(单位：元).有下列表述：

    ①在里程不超过的情况下，出租车费为8元；

    ②若乘车，需支付出租车费20元；

    ③乘车的出租车费为

    ④乘车与出租车费的关系如图所示：

    则正确表述的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求函数f(x)＝x2＋2x＋a－1在区间上的零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业根据供销合同生产某种型号零件10万件，规定：零件长度(单位：毫米)在区间内，则为一等品；若长度在或内，则为二等品；否则为不合格产品.现从生产出的零件中随机抽取100件作样本，其长度数据的频率分布直方图如图所示.

    (1)试估计该样本的平均数；

    (2)根据合同，企业生产的每件一等品可获利10元，每件二等品可获利8元，每件不合格产品亏损6元，若用样本估计总体，试估算该企业生产这批零件所获得的利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】Sn为数列{an}的前n项和，已知an＞0，an2+2an=4Sn+3
    （I）求{an}的通项公式；
    （Ⅱ）设bn= ，求数列{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在斜三棱柱ABC﹣A1B1C1中，侧面ACC1A1⊥底面ABC，底面ABC是等腰直角三角形，CA=CB，A1B⊥AC1 ．
    （1）求证：平面A1BC⊥平面ABC1；
    （2）若直线AA1与底面ABC所成的角为60°，求直线AA1与平面ABC1所成角的正弦值．

    查看答案和解析>>

    同步练习册答案