Question

正方形的顶点和各边中点共8个点，以其中3个点为顶点的等腰三角形共有______个（用数字作答）．

Answer 1

20

解析试题分析：可用分类计数原理去做，按照选点的不同，分为三类，第一类：从正方形的四顶点中选三个点为顶点作三角形，第二类：从正方形的四边中点中选三个点为顶点作三角形，第三类：从正方形的四边中点中选两个点，四顶点中选一个点作三角形，再把每类方法数相加，可得总的方法数解：按题意可分三类．第一类：从正方形的四顶点中选三个点为顶点作三角形，则全为等腰三角形，共有=4种．共有=4种，第三类：从正方形的四边中点中选两个点，四顶点中选一个点作三角形，则每两个中点只能和她们所在边交点，或另两条边交点构成等腰三角形，共有2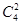=12种，最后，三类方法数相加．得，4+4+12=20种。故答案为20
考点：分类计数原理
点评：本题考查了分类计数原理在排列做和问题中的应用，注意分类依据，要做到不重不漏．