
已知数列{an}的前三项分别为a1=5,a2=6,a3=8,且数列{an}的前n项和Sn满足Sn+m= (S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(1)求数列{an}的通项公式及前n项和Sn;
(2)求满足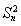 -
-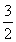 an+33=k2的所有正整数k,n.
an+33=k2的所有正整数k,n.
(1)Sn=n2+3n+1,n∈N*(2)n=10,k=131.
【解析】(1)在等式Sm+n= (S2n+S2m)-(n-m)2中,分别令m=1,m=2,得
(S2n+S2m)-(n-m)2中,分别令m=1,m=2,得
Sn+1= (S2n+S2)-(n-1)2,①
(S2n+S2)-(n-1)2,①
Sn+2=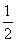 (S2n+S4)-(n-2)2,②
(S2n+S4)-(n-2)2,②
②-①,得an+2=2n-3+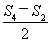 .(3分)
.(3分)
在等式Sn+m=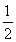 (S2n+S2m)-(n-m2)中,令n=1,m=2,得S3=
(S2n+S2m)-(n-m2)中,令n=1,m=2,得S3= (S2+S4)-1,由题设知,S2=11,S3=19,故S4=29.
(S2+S4)-1,由题设知,S2=11,S3=19,故S4=29.
所以an+2=2n+6(n∈N*),即an=2n+2(n≥3,n∈N*).
又a2=6也适合上式,故an=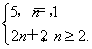 (5分)
(5分)
Sn= 即Sn=n2+3n+1,n∈N*.(6分)
即Sn=n2+3n+1,n∈N*.(6分)
(2)记 -
- an+33=k2(*).
an+33=k2(*).
n=1时,无正整数k满足等式(*).
n≥2时,等式(*)即为(n2+3n+1)2-3(n-10)=k2.(8分)
①当n=10时,k=131.(9分)
②当n>10时,则k<n2+3n+1,
又k2-(n2+3n)2=2n2+3n+31>0,所以k>n2+3n.
从而n2+3n<k<n2+3n+1.
又因为n,k∈N*,所以k不存在,从而无正整数k满足等式(*).(12分)
③当n<10时,则k>n2+3n+1,因为k∈N*,所以k≥n2+3n+2.
从而(n2+3n+1)2-3(n-10)≥(n2+3n+2)2.
即2n2+9n-27≤0.因为n∈N*,所以n=1或2.(14分)
n=1时,k2=52,无正整数解;
n=2时,k2=145,无正整数解.
综上所述,满足等式(*)的n,k分别为n=10,k=131.(16分)


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:解答题
已知等差数列{an}的前n项和Sn满足S3=0,S5=-5.
(1)求{an}的通项公式;
(2)求数列 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:解答题
已知函数f(x)= .
.
(1)求函数f(x)的最小值;
(2)已知m∈R,命题p:关于x的不等式f(x)≥m2+2m-2对任意m∈R恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练D组练习卷(解析版) 题型:解答题
已知无穷数列{an}的各项均为正整数,Sn为数列{an}的前n项和.
(1)若数列{an}是等差数列,且对任意正整数n都有Sn3=(Sn)3成立,求数列{an}的通项公式;
(2)对任意正整数n,从集合{a1,a2,…,an}中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与a1,a2,…,an一起恰好是1至Sn全体正整数组成的集合.
(ⅰ)求a1,a2的值;
(ⅱ)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(解析版) 题型:解答题
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(解析版) 题型:解答题
设向量a=(2,sin θ),b=(1,cos θ),θ为锐角.
(1)若a·b=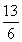 ,求sin θ+cos θ的值;
,求sin θ+cos θ的值;
(2)若a∥b,求sin 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练F组练习卷(解析版) 题型:填空题
定义在实数集上的偶函数f(x)满足f(x+2)=f(x),且f(x)在[-3,-2]上单调递减,又α,β是锐角三角形的两内角,则f(sin α)与f(cos β)的大小关系是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练E组练习卷(解析版) 题型:填空题
当x∈ 时,函数y=sin x+
时,函数y=sin x+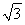 cos x的值域为________.
cos x的值域为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练B组练习卷(解析版) 题型:填空题
在△ABC中,角A,B,C的对边分别是a,b,c,a=8,b=10,△ABC的面积为20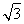 ,则△ABC的最大角的正切值是________.
,则△ABC的最大角的正切值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com