
分析 (Ⅰ)根据数列的递推公式可得数列{$\frac{{a}_{n}}{{2}^{n}}$}是首项为1,公差为1的等差数列,
(Ⅱ)由(Ⅰ)可得数列{$\frac{{a}_{n}}{n}$}是首项为2,公比为2的等比数列,再根据求和公式计算即可.
解答 解:(1)∵a1=2,an+1=2an+2n+1,
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=$\frac{2{a}_{n}+{2}^{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n}}{{2}^{n}}$+1-$\frac{{a}_{n}}{{2}^{n}}$=1,
∵$\frac{{a}_{1}}{2}$=1,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}是首项为1,公差为1的等差数列,
(Ⅱ)由(Ⅰ)可得$\frac{{a}_{n}}{{2}^{n}}$=n,
∴$\frac{{a}_{n}}{n}$=2n,
∴数列{$\frac{{a}_{n}}{n}$}是首项为2,公比为2的等比数列,
故数列{$\frac{{a}_{n}}{n}$}的前n项和Sn=$\frac{2(1-{2}^{n})}{1-2}$=2n+1-2
点评 本题考查了数列的递推公式和等比数列的求和公式,属于基础题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:选择题
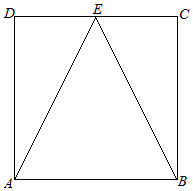 如图,点E是边长为2的正方形ABCD的CD边中点,若向正方形ABCD内随机投掷一点,则所投点落在△ABE内的概率为( )
如图,点E是边长为2的正方形ABCD的CD边中点,若向正方形ABCD内随机投掷一点,则所投点落在△ABE内的概率为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义n!=1×2×3×…×n,例如1!=1,2!=1×2=2,执行右边的程序框图,若输入?=0.01,则输出的e精确到e的近似值为( )
定义n!=1×2×3×…×n,例如1!=1,2!=1×2=2,执行右边的程序框图,若输入?=0.01,则输出的e精确到e的近似值为( )| A. | 2.69 | B. | 2.70 | C. | 2.71 | D. | 2.72 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}$ | B. | $\frac{4}{3}$π | C. | $\frac{9}{2}$π | D. | 9π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图ABC-A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.
如图ABC-A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com