
【题目】已知函数f(x)=lnx﹣ ![]() ,g(x)=
,g(x)= ![]() ﹣1. (Ⅰ)若a>0,试判断f(x)在定义域内的单调性;
﹣1. (Ⅰ)若a>0,试判断f(x)在定义域内的单调性;
(Ⅱ)若f(x)在[1,e]上的最小值为 ![]() ,求a的值;
,求a的值;
(Ⅲ)当a=0时,若x≥1时,恒有xf(x)≤λ[g(x)+x]成立,求λ的最小值.
【答案】解:(Ⅰ)∵f(x)=lnx﹣ ![]() , ∴由题意知f(x)的定义域为(0,+∞)
, ∴由题意知f(x)的定义域为(0,+∞)
且f′(x)= ![]() +
+ ![]() =
= ![]()
∵a>0,∴f′(x)>0,
故f(x)在(0,+∞)上是单调递增函数
(Ⅱ)由(1)可知,f′(x)= ![]() .
.
①若a≥﹣1,则x+a≥0,即f′(x)≥0在[1,e]上恒成立,
此时f(x)在[1,e]上为增函数,
∴f(x)min=f(1)=﹣a= ![]() ,∴a=﹣
,∴a=﹣ ![]() (舍去).
(舍去).
②若a≤﹣e,则x+a≤0,即f′(x)≤0在[1,e]上恒成立,
此时f(x)在[1,e]上为减函数,
∴f(x)min=f(e)=1﹣ ![]() =
= ![]() ,∴a=﹣
,∴a=﹣ ![]() (舍去).
(舍去).
③若﹣e<a<﹣1,令f′(x)=0得x=﹣a,
当1<x<﹣a时,f′(x)<0,∴f(x)在(1,﹣a)上为减函数;
当﹣a<x<e时,f′(x)>0,∴f(x)在(﹣a,e)上为增函数,
∴f(x)min=f(﹣a)=ln(﹣a)+1= ![]() ,∴a=﹣
,∴a=﹣ ![]() .
.
综上所述,a=﹣ ![]() .
.
(Ⅲ)∵xf(x)≤λ[g(x)+x],∴ ![]() ,
,
∴xlnx≤λ( ![]() ),∴lnx﹣
),∴lnx﹣ ![]() (x﹣
(x﹣ ![]() )≤0,
)≤0,
令 ![]() ,
,
当λ≤﹣1时,△=4﹣4(﹣λ)(﹣λ)≤0,故恒有﹣λx2+2x﹣λ≥0,
则G′(x)≥0恒成立,故G(x)在区间[1,+∞)单调递增,
∴G(x)≥G(1)=0,这与条件矛盾;
当﹣1<λ<0时,x=﹣ ![]() ,
,
故有y=﹣λx2+2x﹣λ在区间[1,+∞)上单调递增,
故有﹣λx2+2x﹣λ>2﹣2λ>0,则G′(x)≥0恒成立,
故G(x)在区间[1,+∞)上恒单调递增,
∴G(x)≥G(1)=0,这与条件矛盾;
当λ=0时,G′(x)= ![]() >0,故G(x)在区间[1,+∞)上单调递增,
>0,故G(x)在区间[1,+∞)上单调递增,
∴G(x)≥G(1),这与条件矛盾;
当0<λ<1时,设﹣λx2+2x﹣λ=0的两根为x1 , x2 , 且x1<x2 ,
∵ ![]() ,
,
∴0<x1<1<x2 , ∴x∈(1,x2)时,﹣λx2+2x﹣λ>0,
故函数G(x)在区间(1,x2)上单调递增,
∴G(x2)≥G(1)=0,这与条件矛盾;
当λ≥1时,△=4﹣4(﹣λ)(﹣λ)≤0,故恒有﹣λx2+2x﹣λ≤0,
∴G′(x)≤0恒成立,故G(x)在区间[1,+∞)上单调递减,
∴G(x)≤G(1)=0,命题成立.
综上所述λ≥1,所以λ的最小值为1.
【解析】(Ⅰ)由题意知f(x)的定义域为(0,+∞),且f′(x)= ![]() +
+ ![]() =
= ![]() ,由此得到f(x)在(0,+∞)上是单调递增函数.(Ⅱ)由f′(x)=
,由此得到f(x)在(0,+∞)上是单调递增函数.(Ⅱ)由f′(x)= ![]() ,根据a≥﹣1,a≤﹣e,﹣e<a<﹣1,进行分类讨论,利用导数性质能求出a的值.(Ⅲ)推导出lnx﹣
,根据a≥﹣1,a≤﹣e,﹣e<a<﹣1,进行分类讨论,利用导数性质能求出a的值.(Ⅲ)推导出lnx﹣ ![]() (x﹣
(x﹣ ![]() )≤0,令
)≤0,令 ![]() ,要所λ≤﹣1,﹣1<λ<0,λ=0,0<λ<1,λ≥1进行分类讨论,利用导数性质能求出λ的最小值.
,要所λ≤﹣1,﹣1<λ<0,λ=0,0<λ<1,λ≥1进行分类讨论,利用导数性质能求出λ的最小值.
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若直线ax﹣by+2=0(a>0,b>0)和函数f(x)=ax+1+1(a>0且a≠1)的图象恒过同一个定点,则当 ![]() +
+ ![]() 取最小值时,函数f(x)的解析式是 .
取最小值时,函数f(x)的解析式是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,仅在北京地区每天就有500万单快递等待派送,近5万多名快递员奔跑在一线,快递网点人员流动性也较强,各快递公司需要经常招聘快递员,保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员的每天送货单数统计表:
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 5 | 15 | 25 | 5 | |
已知这两家快递公司的快递员的日工资方案分别为:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元.
元.
(1)分别求甲、乙快递公司的快递员的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)若将频率视为概率,回答下列问题:
①记甲快递公司的快递员的日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣bx+alnx.
(1)若b=2,函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求实数a的取值范围;
(2)在(1)的条件下,证明:f(x2)>﹣ ![]() ;
;
(3)若对任意b∈[1,2],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(﹣3,0),点P在y轴上,点Q在x轴的正半轴上,点N在直线PQ上,且满足 ![]() . (Ⅰ)当点P在y轴上移动时,求点N的轨迹C的方程;
. (Ⅰ)当点P在y轴上移动时,求点N的轨迹C的方程;
(Ⅱ)过点 ![]() 做直线l与轨迹C交于A,B两点,若在x轴上存在一点E(x0 , 0),使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
做直线l与轨迹C交于A,B两点,若在x轴上存在一点E(x0 , 0),使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生 (I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的频数统计图(部分)
运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合要求的可能系较大;
(III)将按程序摆图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.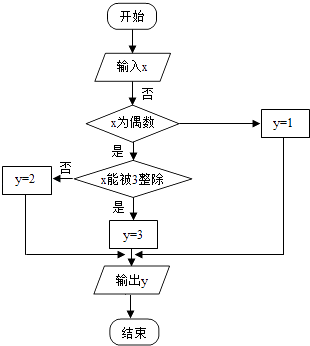
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是求样本x1、x2、…x10平均数 ![]() 的程序框图,图中空白框中应填入的内容为( )
的程序框图,图中空白框中应填入的内容为( ) 
A.S=S+xn
B.S=S+ ![]()
C.S=S+n
D.S=S+ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com