
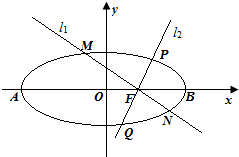
 如图,椭圆的中心在坐标原点,长轴端点为A、B,右焦点为F,且
如图,椭圆的中心在坐标原点,长轴端点为A、B,右焦点为F,且| AF |
| FB |
| OF |
| MP |
| NQ |
| NP |
| MQ |
| AF |
| FB |
| OF |
| MP |
| NQ |
| NP |
| MQ |
 解:(Ⅰ)设椭圆的方程为
解:(Ⅰ)设椭圆的方程为| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
| x2 |
| 2 |
| MP |
| NQ |
| NP |
| MQ |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 4k2 |
| 2k2+1 |
| 2k2-2 |
| 2k2+1 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
(
|
2
| ||
| 2k2+1 |
2
| ||
| 2+k2 |
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 2k2+1 |
2
| ||
| 2+k2 |
| 4 | ||||
2+
|
| 16 |
| 9 |
| 16 |
| 9 |


科目:高中数学 来源: 题型:
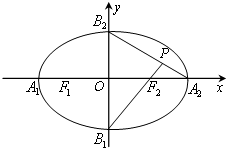 (2013•乌鲁木齐一模)如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为( )
(2013•乌鲁木齐一模)如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为( )查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,椭圆的中心在坐标原点O,左右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率e=
如图,椭圆的中心在坐标原点O,左右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率e=| 3 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,椭圆的中心在坐标原点,F为左焦点,A、B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“优美椭圆”;类比“优美椭圆”,可推出“优美双曲线”的离心率为
如图,椭圆的中心在坐标原点,F为左焦点,A、B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“优美椭圆”;类比“优美椭圆”,可推出“优美双曲线”的离心率为1+
| ||
| 2 |
1+
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2014•江门模拟)如图,椭圆Γ的中心在坐标原点O,过右焦点F(1,0)且垂直于椭圆对称轴的弦MN的长为3.
(2014•江门模拟)如图,椭圆Γ的中心在坐标原点O,过右焦点F(1,0)且垂直于椭圆对称轴的弦MN的长为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com