
【题目】已知数列{an}是公差为2的等差数列,数列{bn}满足 ![]() ,若n∈N*时,anbn+1﹣bn+1=nbn .
,若n∈N*时,anbn+1﹣bn+1=nbn .
(Ⅰ)求{bn}的通项公式;
(Ⅱ)设 ![]() ,求{Cn}的前n项和Sn .
,求{Cn}的前n项和Sn .
【答案】解:(Ⅰ)∵anbn+1﹣bn+1=nbn.
当n=1时,a1b2﹣b2=b1.
∵ ![]() ,
,
∴a1=3,
又∵{an}是公差为2的等差数列,
∴an=2n+1,
则(2n+1)bn+1﹣bn+1=nbn.
化简,得
2bn+1=bn,即 ![]() =
= ![]() ,
,
所以数列{bn}是以1为首项,以 ![]() 为公比的等比数列,
为公比的等比数列,
所以bn=( ![]() )n﹣1;
)n﹣1;
(Ⅱ)由(Ⅰ)知,an=2n+1,
所以 ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
所以Sn=c1+c2+c3+…+cn
= ![]() (
( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
= ![]() (
( ![]() ﹣
﹣ ![]() )
)
= ![]() .
.
【解析】(1)当n=1时,解出![]() ,根据题意得出
,根据题意得出![]() 的通项公式,代入递推公式不难得出
的通项公式,代入递推公式不难得出![]() 的通项公式,(2)写出
的通项公式,(2)写出![]() 的通项公式,进行列项求和,得出
的通项公式,进行列项求和,得出![]() .
.
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系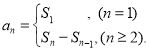 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】某校举行“庆元旦”教工羽毛球单循环比赛(任意两个参赛队只比赛一场),共有高一、高二、高三三个队参赛,高一胜高二的概率为 ![]() ,高一胜高三的概率为
,高一胜高三的概率为 ![]() ,高二胜高三的概率为P,每场胜负独立,胜者记1分,负者记0分,规定:积分相同者高年级获胜.
,高二胜高三的概率为P,每场胜负独立,胜者记1分,负者记0分,规定:积分相同者高年级获胜.
(Ⅰ)若高三获得冠军概率为 ![]() ,求P.
,求P.
(Ⅱ)记高三的得分为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为 ![]() ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,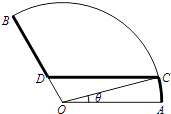
(1)用θ表示CD的长度,并写出θ的取值范围.
(2)当θ为何值时,观光道路最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )
A.32π
B.48π
C.50π
D.64π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆C1:x2+y2=1经过伸缩变换 ![]() 后得到曲线C2以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为cosθ+2sinθ=
后得到曲线C2以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为cosθ+2sinθ= ![]()
(1)求曲线C2的直角坐标方程及直线l的直角坐标方程;
(2)在C2上求一点M,使点M到直线l的距离最小,并求出最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C1是以C1(3,1)为圆心, ![]() 为半径的圆.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线C2:ρsinθ﹣ρcosθ=1.
为半径的圆.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线C2:ρsinθ﹣ρcosθ=1.
(1)求曲线C1的参数方程与直线C2的直角坐标方程;
(2)直线C2与曲线C1相交于A,B两点,求△ABC1的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的左、右焦点分别为F1(﹣c,0)、F2(c,0),过椭圆中心的弦PQ满足|PQ|=2,∠PF2Q=90°,且△PF2Q的面积为1.
的左、右焦点分别为F1(﹣c,0)、F2(c,0),过椭圆中心的弦PQ满足|PQ|=2,∠PF2Q=90°,且△PF2Q的面积为1.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线l不经过点A(0,1),且与椭圆交于M,N两点,若以MN为直径的圆经过点A,求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1+2a2+…+nan=(n﹣1)2n+1+2,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn= ![]() ,Tn=b1+b2+…+bn , 求证:对任意的n∈N* , Tn<
,Tn=b1+b2+…+bn , 求证:对任意的n∈N* , Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将y=cosx的图象上的所有点的纵坐标不变,横坐标缩小到原来的一半,然后再将所得图象向左平移 ![]() 个单位长度,则最后所得图象的解析式为( )
个单位长度,则最后所得图象的解析式为( )
A.y=cos(2x+ ![]() )
)
B.y=cos( ![]() +
+ ![]() )
)
C.y=sin2x
D.y=﹣sin2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com