
【题目】已知二次函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,其中
,其中![]() .
.
(1)求![]() 的值;
的值;
(2)令![]() ,若函数
,若函数![]() 存在极值点,求实数
存在极值点,求实数![]() 的取值范围,并求出极值点.
的取值范围,并求出极值点.
【答案】(I)a=﹣2;(II)解题过程如解析所示
【解析】试题分析:(1)令f(b)-(2b-1)b+b2=1即可解出a;(2)求出φ′(x),令φ′(x)=0,讨论b的符号得出两根与区间(0,1)的关系,从而得出φ(x)的单调性,得出极值的情形.
试题解析:(I)∵f(x)﹣(2b﹣1)x+b2<1的解集为(b,b+1),
即x2+(a﹣2b+1)x+b2+b<0的解集为(b,b+1),
∴方程x2+(a﹣2b+1)x+b2+b=0的解为x1=b,x2=b+1,
∴b+(b+1)=﹣(a﹣2b+1),解得a=﹣2.
(II)φ(x)得定义域为(1,+∞).
由(I)知f(x)=x2﹣2x+b+1,∴g(x)=![]() =x﹣1+
=x﹣1+![]() ,
,
∴φ′(x)=1﹣![]() ﹣
﹣![]() =
=![]() ,
,
∵函数φ(x)存在极值点,∴φ′(x)=0有解,
∴方程x2﹣(2+k)x+k﹣b+1=0有两个不同的实数根,且在(1,+∞)上至少有一根,
∴△=(2+k)2﹣4(k﹣b+1)=k2+4b>0.
解方程x2﹣(2+k)x+k﹣b+1=0得x1=![]() ,x2=
,x2=![]()
(1)当b>0时,x1<1,x2>1,
∴当x∈(1,![]() )时,φ′(x)<0,当x∈(
)时,φ′(x)<0,当x∈(![]() ,+∞)时,φ′(x)>0,
,+∞)时,φ′(x)>0,
∴φ(x)在(1,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴φ(x)极小值点为![]()
(2)当b<0时,由△=k2+4b>0得k<﹣2![]() ,或k>2
,或k>2![]() ,
,
若k<﹣2![]()
![]() ,则x1<1,x2<1,
,则x1<1,x2<1,
∴当x>1时,φ′(x)>0,∴φ(x)在(1,+∞)上单调递增,不符合题意;
若k>2![]()
![]() ,则x1>1,x2>1,
,则x1>1,x2>1,
∴φ(x)在(1,![]() )上单调递增,在(
)上单调递增,在(![]() ,
,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)单调递增,
,+∞)单调递增,
∴φ(x)的极大值点为![]() ,极小值点为
,极小值点为![]() .
.
综上,当b>0时,k取任意实数,函数φ(x)极小值点为![]() ;
;
当b<0时,k>2![]() ,函数φ(x)极小值点为
,函数φ(x)极小值点为![]() ,极大值点为
,极大值点为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图2所示.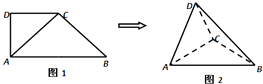
(1)求证:BC⊥平面ACD;
(2)求几何体D﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,f(﹣2)=2,对任意x∈R,f′(x)>2,则f(x)>2x+6的解集为( )
A.(﹣2,2)
B.(﹣∞,﹣2)
C.(﹣2,+∞)
D.(﹣∞,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,函数 ![]() ,
,
(1)求函数f(x)的定义域;
(2)将函数y=f(x)的图象向右平移两个单位后得到函数y=g(x)的图象,若实数x满足g(x)≥0,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1的侧面ACC1A1是正方形,AC=BC,点O是侧面ACC1A1的中心,∠ACB= ![]() ,M在棱BC上,且MC=2BM=2.
,M在棱BC上,且MC=2BM=2. 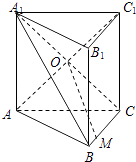
(1)证明BC⊥AC1;
(2)求OM的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com