【题目】某地区经过一年的新农村建设，农村的经济收入增加了一倍．实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例．得到如下饼图：
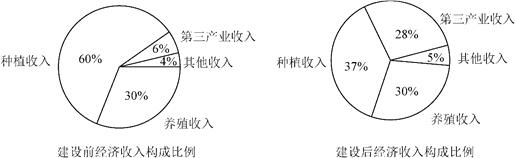
则下面结论中不正确的是
A. 新农村建设后，种植收入减少
B. 新农村建设后，其他收入增加了一倍以上
C. 新农村建设后，养殖收入增加了一倍
D. 新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半
【答案】A
【解析】分析：首先设出新农村建设前的经济收入为M，根据题意，得到新农村建设后的经济收入为2M，之后从图中各项收入所占的比例，得到其对应的收入是多少，从而可以比较其大小，并且得到其相应的关系，从而得出正确的选项.
详解：设新农村建设前的收入为M，而新农村建设后的收入为2M，
则新农村建设前种植收入为0.6M，而新农村建设后的种植收入为0.74M，所以种植收入增加了，所以A项不正确；
新农村建设前其他收入我0.04M，新农村建设后其他收入为0.1M，故增加了一倍以上，所以B项正确；
新农村建设前，养殖收入为0.3M，新农村建设后为0.6M，所以增加了一倍，所以C项正确；
新农村建设后，养殖收入与第三产业收入的综合占经济收入的
，所以超过了经济收入的一半，所以D正确；
故选A.
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目：高中数学 来源： 题型：
【题目】已知圆C经过P(4，－2)，Q(－1，3)两点，且圆心C在直线x＋y－1＝0上．
(1)求圆C的方程；
(2)若直线l∥PQ，且l与圆C交于点A，B且以线段AB为直径的圆经过坐标原点，求直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
．
（1）求函数
的最小正周期和对称轴方程；
（2）若
，求的值域．
【答案】（1）对称轴为
，最小正周期
；（2）
【解析】
(1)利用正余弦的二倍角公式和辅助角公式将函数解析式进行化简得到
，由周期公式和对称轴公式可得答案；(2)由x的范围得到
，由正弦函数的性质即可得到值域.
（1）
令
，则
的对称轴为，最小正周期；
（2）当时，，
因为
在
单调递增，在
单调递减，
在
取最大值，在
取最小值，
所以
，
所以．
【点睛】
本题考查正弦函数图像的性质，考查周期性，对称性，函数值域的求法，考查二倍角公式以及辅助角公式的应用，属于基础题.
【题型】解答题
【结束】
21
【题目】已知等比数列
的前
项和为
，公比
，
，
．
（1）求等比数列的通项公式；
（2）设
，求
的前项和
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某村电费收取有以下两种方案供农户选择：
方案一：每户每月收取管理费2元，月用电量不超过30度时，每度0.5元；超过30度时，超过部分按每度0.6元收取；
方案二：不收管理费，每度0.58元．
（1）求方案一
收费（元）与用电量
（度）间的函数关系；
（2）老王家九月份按方案一交费35元，问老王家该月用电多少度？
（3）老王家该月用电量在什么范围内，选择方案一比选择方案二更好？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)对任意x，y∈R，总有f(x)＋f(y)＝f(x＋y)，且当x>0时，f(x)<0，f(1)＝－
.
(1)求证：f(x)是R上的单调减函数．
(2)求f(x)在[－3,3]上的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线的参数方程为 
（t为参数），其中p＞0，焦点为F，准线为l．过抛物线上一点M作l的垂线，垂足为E．若|EF|=|MF|，点M的横坐标是3，则p= ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=sin（2x+ 
）+sin（2x﹣ ）+2cos2x﹣1，x∈R．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）在区间[ 
]上的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知关于x的一元二次方程x2﹣（2m+3）x+m2+2＝0．
（1）若方程有实数根，求实数m的取值范围；
（2）若方程两实数根分别为x1、x2，且满足x12+x22＝31+|x1x2|，求实数m的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
