【答案】
分析:(1)f(x)<0,可化为x
2-(c+1)x+c=(x-1)(x-c)<0,对c分类讨论,即可得到不等式的解集;
(2)当c=-2时,f(x)>ax-5在(0,2)上恒成立,等价于x
2+x-2>ax-5在(0,2)上恒成立,即ax<x
2+x+3在(0,2)上恒成立,分离参数,求最值,即可求实数a的取值范围;
(3)利用0<g(2)<1,3<g(3)<5,建立不等式,将g(4)用g(2),g(3)表示,即可求g(4)的范围.
解答:解:(1)∵f(x)<0,∴x
2-(c+1)x+c=(x-1)(x-c)<0…(1分)
①当c<1时,c<x<1
②当c=1时,(x-1)
2<0,∴x∈φ
③当c>1时,1<x<c…(3分)
综上,当c<1时,不等式的解集为{x|c<x<1},当c=1时,不等式的解集为φ,当c>1时,不等式的解集为{x|1<x<c}. …(4分)
(2)当c=-2时,f(x)>ax-5在(0,2)上恒成立,等价于x
2+x-2>ax-5在(0,2)上恒成立,
即ax<x
2+x+3在(0,2)上恒成立,
∴a<(
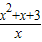
)
min,
设g(x)=
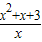
,则g(x)=
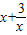
+1≥2

+1
当且仅当
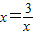
,即x=
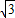
∈(0,2)时,等号成立
∴g(x)
min=2
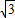
+1
∴a<2
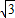
+1;
(3)∵g(2)=f(2)-2a=2-c-2a,∴0<2-c-2a<1
∴1<c+2a<2
∵g(3)=f(3)-3a=6-2c-3a,∴3<2-c-2a<5,∴1<2c+3a<3…(10分)
∵g(4)=f(4)-4a=12-3c-4a
设-3c-4a=x(c+2a)+y(2c+3a)=(x+2y)c+(2x+3y)a…(11分)
∴
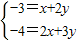
,∴
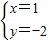
…(12分)
∴-3c-4a=x(c+2a)+y(2c+3a)=(c+2a)+[-2(2c+3a)]
∵1<c+2a<2-6<-2(2c+3a)<-2,∴
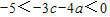
,∴
\end{array}\right.7<12-3c-4a<12…(13分)
∴7<g(4)<12…(14分)
点评:本题考查解不等式,考查函数恒成立问题,考查学生分析解决问题的能力,属于中档题.

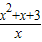 )min,
)min,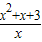 ,则g(x)=
,则g(x)=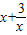 +1≥2
+1≥2 +1
+1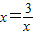 ,即x=
,即x=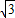 ∈(0,2)时,等号成立
∈(0,2)时,等号成立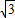 +1
+1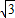 +1;
+1;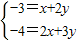 ,∴
,∴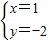 …(12分)
…(12分)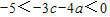 ,∴…(13分)
,∴…(13分)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<