
| A. | $\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 1+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
分析 求出抛物线的焦点和准线,运用向量的平方即为模的平方,可得|PF2|=2,由抛物线的定义,可得P的横坐标,可得P的坐标,运用双曲线的定义和离心率公式,计算即可得到所求值.
解答 解:抛物线y2=4x的焦点为(1,0),准线为x=-1,
设P(m,n),
若($\overrightarrow{{F}_{2}P}$+$\overrightarrow{{F}_{2}{F}_{1}}$)•($\overrightarrow{{F}_{2}P}$-$\overrightarrow{{F}_{2}{F}_{1}}$)=0,
则$\overrightarrow{{F}_{2}P}$2-$\overrightarrow{{F}_{2}{F}_{1}}$2=0,
由F1(-1,0),F2(1,0),可得|F1F2|=2,
即有|PF2|=2,
由抛物线的定义可得xP+1=2,即有xP=1,
可得P(1,±2),
由双曲线的定义可得|PF1|-|PF2|=$\sqrt{(1+1)^{2}+{2}^{2}}$-$\sqrt{{2}^{2}}$=2$\sqrt{2}$-2,
可得双曲线的a=$\sqrt{2}$-1,c=1,
可得e=$\frac{c}{a}$=1+$\sqrt{2}$.
故选:B.
点评 本题考查双曲线的离心率的求法,考查抛物线的定义、方程和性质,以及向量的平方即为模的平方,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
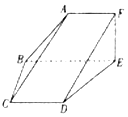 如图,平面ABEF⊥平面CBED,四边形ABEF为直角梯形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.
如图,平面ABEF⊥平面CBED,四边形ABEF为直角梯形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
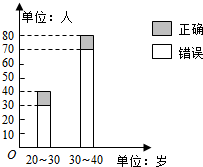 “开门大吉”是某电视台推出的游戏节目,选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
“开门大吉”是某电视台推出的游戏节目,选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=(-2x+3)ex | B. | f(x)=e-2x+3 | ||
| C. | $f(x)={e^{-{x^2}+3x+1}}$ | D. | $f(x)=(-2x+3){e^{-{x^2}+3x+1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com