
 |2的所有取值之和;
|2的所有取值之和; |2取得最大值”的概率.
|2取得最大值”的概率.科目:高中数学 来源:不详 题型:解答题
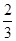 ,乙队获胜的概率为
,乙队获胜的概率为 ,假设每场比赛的结果互相独立.现已赛完两场,乙队以
,假设每场比赛的结果互相独立.现已赛完两场,乙队以 暂时领先.
暂时领先. ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.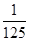 | B. | C. | D.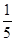 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com