
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
已知抛物线 ,F是焦点,直线l是经过点F的任意直线.
,F是焦点,直线l是经过点F的任意直线.
(1)若直线l与抛物线交于两点A、B,且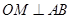 (O是坐标原点,M是垂足),求动点M的轨迹方程;
(O是坐标原点,M是垂足),求动点M的轨迹方程;
(2)若C、D两点在抛物线 上,且满足
上,且满足 ,求证直线CD必过定点,并求出定点的坐标.
,求证直线CD必过定点,并求出定点的坐标.
所求动点M的轨迹方程是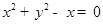 (
( ).
).
直线CD的方程可化为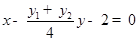 .
直线CD恒过定点,且定点坐标为(2,0).
.
直线CD恒过定点,且定点坐标为(2,0).
【解析】(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
解 (1) 设动点M的坐标为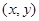 .
…………………1分
.
…………………1分
∵抛物线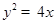 的焦点是
的焦点是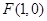 ,直线l恒过点F,且与抛物线交于两点A、B,
,直线l恒过点F,且与抛物线交于两点A、B,
又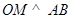 ,
,
∴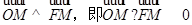 .
…………………3分
.
…………………3分
∴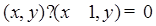 ,化简,得
,化简,得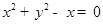 . …………………5分
. …………………5分
又当M与原点重合时,直线l与x轴重合,故 .
.
∴所求动点M的轨迹方程是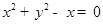 (
( ).
).
(2) 设点C、D的坐标为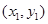 、
、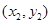 . …………………………6分
. …………………………6分
∵C、D在抛物线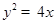 上,
上,
∴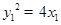 ,
,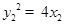 ,即
,即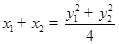 ,
,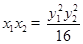 .
.
又 ,
,
∴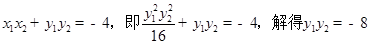 . ………8分
. ………8分
∵点C、D的坐标为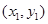 、
、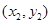 ,
,
∴直线CD的一个法向量是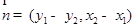 ,可得直线CD的方程为:
,可得直线CD的方程为:
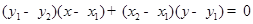 ,化简,得
,化简,得
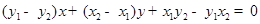 ,进一步用
,进一步用 ,有
,有
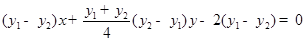 .
.
又抛物线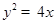 上任两点的纵坐标都不相等,即
上任两点的纵坐标都不相等,即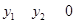 .
.
∴直线CD的方程可化为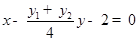 . ………………………10分
. ………………………10分
∴直线CD恒过定点,且定点坐标为(2,0). ………………………12分


科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第五次联考理数 题型:解答题
.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数 为偶函数, 且
为偶函数, 且
(1)求 的值;
的值;
(2)若 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:
 ,
, ,…,
,…,  后得到如下频率分布直方图.
后得到如下频率分布直方图.

(Ⅰ)求分数在 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样 本看成一个总体,从中任意选取2人, 求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源:2014届吉林长春外国语学校高一下学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分12分)

本公司计划2012年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年陕西省、西工大附中高三第五次联考理数 题型:解答题
.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数 为偶函数, 且
为偶函数, 且
(1)求 的值;
的值;
(2)若 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011年上海市高二第一学期期末考试数学试卷 题型:解答题
(本小题满分12分)
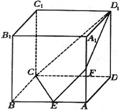
如图,长方体 中, AD=2,AB=AD=4,
中, AD=2,AB=AD=4, ,点E是AB的中点,点F是
,点E是AB的中点,点F是 的中点。
的中点。
(1)求证: ;
;
(2)求异面直线 与
与 所成的角的大小;
所成的角的大小;
(本题满分12分)
已知 ,且以下命题都为真命题:
,且以下命题都为真命题:
命题 实系数一元二次方程
实系数一元二次方程 的两根都是虚数;
的两根都是虚数;
命题 存在复数
存在复数 同时满足
同时满足 且
且 .
.
求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com