
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处切线的斜率为
处切线的斜率为![]() ,判断函数
,判断函数![]() 的单调性;
的单调性;
(2)若函数![]() 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)对![]() 求导,根据导数的几何意义代入
求导,根据导数的几何意义代入![]() ,可求得切线的斜率,进而可得a的值;分别判断当
,可求得切线的斜率,进而可得a的值;分别判断当![]() 、
、![]() 时,
时,![]() 的正负,即可判断
的正负,即可判断![]() 的单调性;
的单调性;
(2)当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,分别求出
,分别求出![]() 、
、![]() 和
和![]() 时,
时,![]() 的单调性,并求出极值个数;当
的单调性,并求出极值个数;当![]() 时,由
时,由![]() 得
得![]() ,判断
,判断![]() 的单调性,可得
的单调性,可得![]() ,又
,又![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,综合分析,即可得答案.
,综合分析,即可得答案.
(1)由题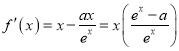 ,
,
则![]() ,得
,得![]() ,
,
此时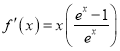 ,由
,由![]() 得
得![]() .
.
则![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;![]() 时,
时,![]() ,
,![]() 为增函数,且
为增函数,且![]() ,所以
,所以![]() 为R上的增函数.
为R上的增函数.
(2)①当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
若![]() ,由(1)知,
,由(1)知,![]() 为R上的增函数.
为R上的增函数.
由![]() ,
,![]() ,
,
所以![]() 只有一个零点,不符合题意.
只有一个零点,不符合题意.
若![]() ,则
,则![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;![]() 时,
时,![]() ,
,![]() 为增函数.
为增函数.
而![]() ,故
,故![]() 最多只有一个零点,不符合题意.
最多只有一个零点,不符合题意.
若![]() 时,则
时,则![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;![]() 时,
时,![]() ,
,![]() 为增函数.
为增函数.
得![]() ,故
,故![]() 最多只有一个零点,不符合题意.
最多只有一个零点,不符合题意.
②当![]() 时,由
时,由![]() 得
得![]() ,
,
由![]() 得
得![]() ,
,![]() 为减函数,由
为减函数,由![]() 得
得![]() ,
,![]() 为增函数,
为增函数,
则![]() .又
.又![]() ,
,
![]() ,
,
所以当![]() 时,
时,![]() 始终有两个零点.
始终有两个零点.
综上所述,a的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】十九大提出:坚决打赢脱贫攻坚战,做到精准扶贫.某县积极引导农民种植一种名贵中药材,从而大大提升了该县村民的经济收入.2019年年底,该机构从该县种植的这种名贵药材的农户中随机抽取了100户,统计了他们2019年因种植,中药材所获纯利润(单位:万元)的情况(假定农户因种植中药材这一项一年最多获利11万元),统计结果如下表所示:
![]()
(1)由表可以认为,该县农户种植中药材所获纯利润Z(单位:万元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值),
(每组数据取区间的中点值),![]() 近似为样本方差
近似为样本方差![]() .若该县有1万户农户种植了该中药材,试估算所获纯利润Z在区间(1.9,8.2)的户数;
.若该县有1万户农户种植了该中药材,试估算所获纯利润Z在区间(1.9,8.2)的户数;
(2)为答谢广大农户的积极参与,该调查机构针对参与调查的农户举行了抽奖活动,抽奖规则如下:在一箱子中放置5个除颜色外完全相同的小球,其中红球1个,黑球4个.让农户从箱子中随机取出一个小球,若取到红球,则抽奖结束;若取到黑球,则将黑球放回箱中,让他继续取球,直到取到红球为止(取球次数不超过10次).若农户取到红球,则视为中奖,获得2000元的奖励,若一直未取到红球,则视为不中奖.现农户张明参加了抽奖活动,记他中奖时取球的次数为随机变量X,他取球的次数为随机变量Y.
①证明:![]() 为等比数列;
为等比数列;
②求Y的数学期望.(精确到0.001)
参考数据:![]() .若随机变量
.若随机变量![]() 则
则![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课外兴趣小组利用假期到植物园开展社会实践活动,研究某种植物生长情况与温度的关系.现收集了该种植物月生长量y(cm)与月平均气温x(℃)的8组数据,并制成如图所示的散点图.
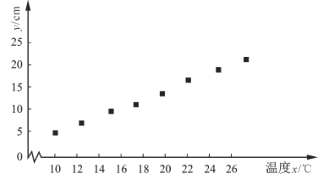
根据收集到的数据,计算得到如下值:
|
|
|
|
18 | 12.325 | 224.04 | 235.96 |
(1)求出y关于x的线性回归方程(最终结果的系数精确到0.01),并求温度为28℃时月生长量y的预报值;
(2)根据y关于x的回归方程,得到残差图如图所示,分析该回归方程的拟合效果.

附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

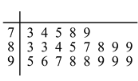
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,①已知点
中,①已知点![]() ,直线
,直线![]() :
:![]() ,动点
,动点![]() 满足到点
满足到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() ;②已知圆
;②已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 为圆
为圆![]() 的切线,记点
的切线,记点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,动点
,动点![]() 满足
满足![]() ;③点
;③点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上运动,且
轴上运动,且![]() ,动点
,动点![]() 满足
满足![]() .
.
(1)在①,②,③这三个条件中任选一个,求动点![]() 的轨迹方程;
的轨迹方程;
(2)记(1)中的轨迹为![]() ,经过点
,经过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴相交于点
轴相交于点![]() ,求点
,求点![]() 纵坐标的取值范围.
纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点
,点![]() 是抛物线
是抛物线![]() 的焦点,过点F作直线
的焦点,过点F作直线![]() 交抛物线于M,N两点,延长
交抛物线于M,N两点,延长![]() ,
,![]() 分别交椭圆于A,B两点,记
分别交椭圆于A,B两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,
,![]() .
.
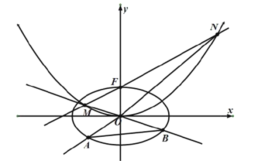
(1)求![]() 的值及抛物线的准线方程;
的值及抛物线的准线方程;
(2)求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右两个焦点为
的左,右两个焦点为![]() 、
、![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 有公共焦点
有公共焦点![]() .且两曲线
.且两曲线![]() 、
、![]() 在第一象限的交点
在第一象限的交点![]() 的横坐标为
的横坐标为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 的交点为
的交点为![]() 、
、![]() (
(![]() 为坐标原点),与椭圆
为坐标原点),与椭圆![]() 的交点为
的交点为![]() 、
、![]() (
(![]() 在线段
在线段![]() 上),且
上),且![]() .问满足条件的直线
.问满足条件的直线![]() 有几条,说明理由.
有几条,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com