
| A. | 截距相等的直线都可以用方程$\frac{x}{a}+\frac{y}{a}=1$表示 | |
| B. | 方程x+my-2=0(m∈R)不能表示平行y轴的直线 | |
| C. | 经过点P(1,1),倾斜角为θ的直线方程为y-1=tanθ(x-1) | |
| D. | 经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线方程为$y-{y_1}=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}(x-{x_1})$ |
分析 A,截距相等为0的直线都不可以用方程$\frac{x}{a}+\frac{y}{a}=1$表示;
B,当m=0时,方程x+my-2=0(m∈R)表示平行y轴的直线;
C,倾斜角为θ=900的直线方程不能写成点斜式;
D,x1≠x2,直线的斜率存在,可以用点斜式表示.
解答 解:对于A,截距相等为0的直线都不可以用方程$\frac{x}{a}+\frac{y}{a}=1$表示,故错;
对于B,当m=0时,方程x+my-2=0(m∈R)表示平行y轴的直线x=2,故错;
对于C,经过点P(1,1),倾斜角为θ=900的直线方程不能写成y-1=tanθ(x-1),故错;
对于D,∵x1≠x2,∴直线的斜率存在,可写成 $y-{y_1}=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}(x-{x_1})$,故正确;
故选:D.
点评 本题考查了命题真假的判定,涉及了直线方程的性质,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,9] | B. | [1,+∞) | C. | [1,9)∪(9,+∞) | D. | (9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\root{3}{4}$ | B. | $\root{3}{4}$ | C. | 4$\root{3}{3}$ | D. | $\root{3}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{2},\sqrt{2})$ | B. | $(1,\sqrt{2})$ | C. | $(-1,\sqrt{2}]$ | D. | $[1,\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
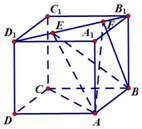 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且$EF=\frac{{\sqrt{2}}}{2}$,则下列结论中正确的是①②③④.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且$EF=\frac{{\sqrt{2}}}{2}$,则下列结论中正确的是①②③④.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com