
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
: ![]() 的左焦点是
的左焦点是![]() ,离心率为
,离心率为![]() ,且
,且![]() 上任意一点
上任意一点![]() 到
到![]() 的最短距离为
的最短距离为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() (不过原点)与
(不过原点)与![]() 交于两点
交于两点![]() 、
、![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.
(i)证明:直线![]() 与
与![]() 的斜率乘积为定值;
的斜率乘积为定值;
(ii)求![]() 面积的最大值及此时
面积的最大值及此时![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)(i)见解析;(ii)
;(2)(i)见解析;(ii)![]() 面积的最大值是
面积的最大值是![]() ,此时
,此时![]() 的斜率为
的斜率为![]() .
.
【解析】试题分析:(1)由题设可以得到关于![]() 的方程组为
的方程组为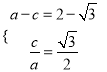 ,从而
,从而 ,故
,故![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .(2)设直线
.(2)设直线![]() 为:
为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,联立直线的方程和椭圆的方程并消元后可以得到
,联立直线的方程和椭圆的方程并消元后可以得到![]() ,利用韦达定理得到
,利用韦达定理得到![]() ,故
,故![]() ,从而
,从而![]() 为定值.利用弦长公式和点到直线的距离可得
为定值.利用弦长公式和点到直线的距离可得![]() ,令
,令![]() ,从而
,从而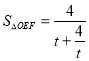 ,最后利用基本不等式可以得到面积的最大值为
,最后利用基本不等式可以得到面积的最大值为![]() 且此时
且此时![]() 也就是
也就是![]() .
.
解析:(1)由题意得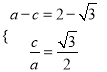 ,解得
,解得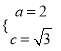 ,∴
,∴![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)(i)设直线![]() 为:
为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由题意得
,由题意得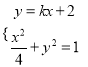 ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,由韦达定理得:
,由韦达定理得: ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,∴直线
,∴直线![]() 与
与![]() 的斜率乘积为定值.
的斜率乘积为定值.

(ii)由(i)可知: ![]()
![]()
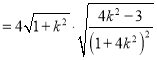
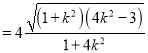 ,又点
,又点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴![]() 的面积
的面积![]()
![]()

![]() ,令
,令![]() ,则
,则![]() ,∴
,∴![]()
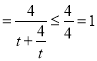 ,当且仅当
,当且仅当![]() 时等号成立,此时
时等号成立,此时![]() ,且满足
,且满足![]() ,∴
,∴![]() 面积的最大值是
面积的最大值是![]() ,此时
,此时![]() 的斜率为
的斜率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数(x)=xlnx,g(x)=ax3-![]() .
.
(Ⅰ)求函数(x)的单调递增区间和最小值;
(Ⅱ)若函数y= (x)与函数y =g(x)的图象在交点处存在公共切线,求实数a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 、
、![]() 为常数).若函数
为常数).若函数![]() 与
与![]() 的图象在
的图象在![]() 处相切,
处相切,
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设函数![]()
![]() ,若
,若![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅲ)设函数![]() ,若
,若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)若过![]() 、
、![]() 、
、![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() :
: ![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(III)在(Ⅱ)的条件下,过右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() 使得以
使得以![]() 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出![]() 的取值范围,如果不存在,说明理由
的取值范围,如果不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 人数(单位:人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 为椭圆
为椭圆 ![]() 上任一点,
上任一点,![]() ,
,![]() 为椭圆的焦点,
为椭圆的焦点,![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆的标准方程;
(2)直线 ![]() 经过点
经过点 ![]() ,且与椭圆交于
,且与椭圆交于 ![]() ,
,![]() 两点,若直线
两点,若直线 ![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,经研究发现鲑鱼的游速可以表示为函数y=![]() log3(
log3(![]() ),单位是m/s,θ是表示鱼的耗氧量的单位数.
),单位是m/s,θ是表示鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是900个单位时,它的游速是多少?
(2)计算一条鱼静止时耗氧量的单位数。
(3)某条鲑鱼想把游速提高1 m/s,那么它的耗氧量的单位数是原来的多少倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com