
【题目】定义在区间D上的函数f(x),如果满足:对任意x∈D,都存在常数M≥0,有|f(x)|≤M,则称f(x)是区间D上有界函数,其中M称为f(x)上的一个上界,已知函数g(x)=log ![]() 为奇函数.
为奇函数.
(1)求函数g(x)在区间[ ![]() ,
, ![]() ]上的所有上界构成的集合;
]上的所有上界构成的集合;
(2)若g(1﹣m)+g(1﹣m2)<0,求m的取值范围.
【答案】
(1)解:∵函数g(x)=log ![]() 为奇函数.
为奇函数.
∴g(﹣x)=﹣g(x),
即log ![]() =﹣log
=﹣log ![]()
∴ ![]() =
= ![]() ,1﹣x2=1﹣a2x2
,1﹣x2=1﹣a2x2
得出;a=±1,而a=1时不符合题意,
故a=﹣1,
函数g(x)=log ![]() (
( ![]() ﹣1)是减函数,在区间[
﹣1)是减函数,在区间[ ![]() ,
, ![]() ]上是单调递减,
]上是单调递减,
g( ![]() )=﹣1,g(
)=﹣1,g( ![]() )=﹣2,|g(x)|≤2
)=﹣2,|g(x)|≤2
所以g(x)在区间[ ![]() ,
, ![]() ]上的所有上界构成的集合[2,+∞)
]上的所有上界构成的集合[2,+∞)
(2)解:g(1﹣m)+g(1﹣m2)<0,g(1﹣m)<g(m2﹣1),
g(x)为减函数,
所以有﹣1<m2﹣1<1﹣m<1,
解得0<m<1,
故不等式的解集{m|0<m<1}.
【解析】(1)利用奇函数的性质,求出函数的解析式,利用单调性求函数g(x)在区间[ ![]() ,
, ![]() ]上的所有上界构成的集合;(2)若g(1﹣m)+g(1﹣m2)<0,有﹣1<m2﹣1<1﹣m<1,即可求m的取值范围.
]上的所有上界构成的集合;(2)若g(1﹣m)+g(1﹣m2)<0,有﹣1<m2﹣1<1﹣m<1,即可求m的取值范围.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】若圆C1:(x﹣1)2+(y+3)2=1与圆C2:(x﹣a)2+(y﹣b)2=1外离,过直线l:x﹣y﹣1=0上任意一点P分别做圆C1 , C2的切线,切点分别为M,N,且均保持|PM|=|PN|,则a+b=( )
A.﹣2
B.﹣1
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足(an+1﹣1)(an﹣1)=3(an﹣an+1),a1=2,令bn= ![]() .
.
(1)求数列{bn}的通项公式;
(2)求数列{bn3n}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( ) 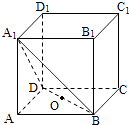
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x+4y﹣4=0,是否存在斜率为1的直线l,使l被圆C截得的弦长AB为直径的圆过原点,若存在求出直线的方程l,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种零件按质量标准分为1,2,3,4,5五个等级,现从批该零件中随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
(1)在抽取的20个零件中,等级为5的恰有2个,求m,n的值;
(2)在(1)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,EF∩AC=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图2所示五棱锥P﹣ABFED,且AP= ![]() ,
, 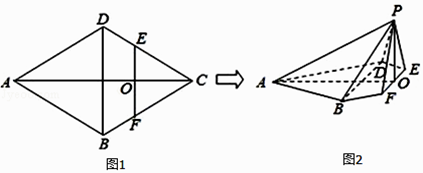
(1)求证:BD⊥平面POA;
(2)求二面角B﹣AP﹣O的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com