
【题目】若函数![]() 在处的切线与直线
在处的切线与直线![]() 平行,则实数
平行,则实数![]() ____;
____;
当a≤0时,若方程![]() 有且只有一个实根,则实数的取值范围为_________.
有且只有一个实根,则实数的取值范围为_________.
【答案】 1 ![]()
【解析】 (1)由f(x)=x3+3ax1,得到f′(x)=3x2+3a,
因为曲线在x=1处的切线与y=6x+6平行,
而y=6x+6的斜率为6,
所以f′(1)=6,即3+3a=6,解得a=1;
(2)令g(x)=x3+3ax16,
g′(x)=3x2+3a=3(x2+a),
a=0时,g′(x)0,g(x)在R递增,
而x→∞时,g(x)→∞,x→+∞时,g(x)→+∞,
故函数g(x)有且只有一个零点,
即方程f(x)=15有且只有一个实根,
a<0时,令g′(x)>0,解得: ![]() 或
或![]() ,
,
令g′(x)<0,解得: ![]() ,
,
则g(x)在![]() 递增,在
递增,在![]() 递减,在
递减,在![]() 递增,
递增,
故g(x)极大值![]() ,
,
解得: ![]() ,
,
综上:-4<a0.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(1)求曲线![]() 与
与![]() 的交点
的交点![]() 的直角坐标;
的直角坐标;
(2)设点![]() ,
, ![]() 分别为曲线
分别为曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某市地产数据研究的数据显示,2016年该市新建住宅销售均价走势如下图所示,为抑制房价过快上涨,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.
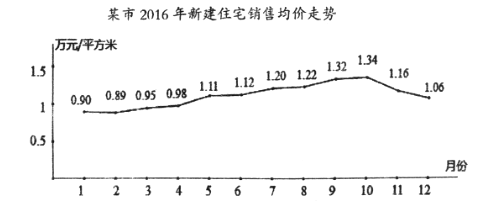
(1)地产数据研究院发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
(2)地产数据研究院在2016年的12个月份中,随机抽取三个月的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
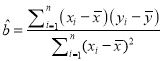 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一
人答一份).现从回收的年龄在20~60岁的问卷中随机抽取了100份,统计结果如下面的图表所示.
年龄 分组 | 抽取份数 | 答对全卷 的人数 | 答对全卷的人数 占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) |
| 27 | 0.9 |
[40,50) | 10 | 4 |
|
[50,60] | 20 |
| 0.1 |

(1)分别求出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)从年龄在![]() 答对全卷的人中随机抽取2人授予“环保之星”,求年龄在
答对全卷的人中随机抽取2人授予“环保之星”,求年龄在![]() 的人中至少有1人被授予“环保之星”的概率.
的人中至少有1人被授予“环保之星”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com