
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,![]() ,∠ABC=∠BCD=90°,E为PB的中点。
,∠ABC=∠BCD=90°,E为PB的中点。

(1)证明:CE∥面PAD.
(2)若直线CE与底面ABCD所成的角为45°,求四棱锥P-ABCD的体积。
【答案】(1)见解析(2)![]()
【解析】
(1)取PA中点Q,连接QD,QE,可证四边形CDQE为平行四边形,从而CE∥QD,于是证得线面平行;
(2)连接BD,取BD中点O,连接EO,CO,可证EO∥PD,从而得到直线CE与底面ABCD所成的角,求得EO也即能求得PD,最终可得棱锥体积.
解法一:(1)取PA中点Q,连接QD,QE,
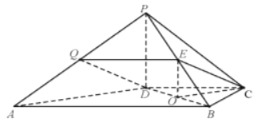
则QE∥AB,且QE=![]() AB
AB
∴QE∥CD,且QE=CD.
即四边形CDQE为平行四边形,CE∥QD.
又∵CE![]() 平面PAD,QD
平面PAD,QD![]() 平面PAD,
平面PAD,
∴CE∥平面PAD.
(2)连接BD,取BD中点O,连接EO,CO
则EO∥PD,且EO=![]() PD.
PD.
∵PD⊥平面ABCD,
∴EO⊥平面ABCD.
则CO为CE在平面ABCD上的射影,
即∠ECO为直线CE与底面ABCD所成的角,∠ECO=45°
在等腰直角三角形BCD中,BC=CD=2,则BD=2![]() ,
,
则在RtΔECO中,∠ECO=45°,EO=CO=![]() BD=
BD=![]()
2PD=2E0=2![]() ,
,
∴![]()
∴![]()
∴四棱锥P-ABCD的体积为![]() .
.
解法二:(1)取AB中点Q,连接QC,QE
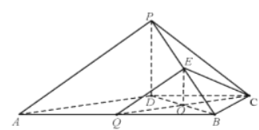
则QE∥PA
∵PA![]() 平面PAD,QE
平面PAD,QE![]() 平面PAD
平面PAD
∴QE∥平面PAD,
又∵AQ=
∴四边形AQCDカ平行四迹形,
则CQ∥DA
∵DA![]() 平面PAD,CQ
平面PAD,CQ![]() 平面PAD,
平面PAD,
∴CQ∥平面PAD,
(QE∥平面PAD.CQ∥平面PAD,证明其中一个即给2分)
又QE![]() 平面CEQ,CQ
平面CEQ,CQ![]() 平面CEQ,QE
平面CEQ,QE![]() CQ=Q,
CQ=Q,
∴平面CEQ∥平面PAD,
又CE![]() 平面CQ,
平面CQ,
∴CE∥平面PAD.
(2)同解法一.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级![]() 名学生中进行了抽样调查,发现喜欢甜品的占
名学生中进行了抽样调查,发现喜欢甜品的占![]() .这
.这![]() 名学生中南方学生共
名学生中南方学生共![]() 人。南方学生中有
人。南方学生中有![]() 人不喜欢甜品.
人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有![]() 名数学系的学生,其中
名数学系的学生,其中![]() 名不喜欢甜品;有
名不喜欢甜品;有![]() 名物理系的学生,其中
名物理系的学生,其中![]() 名不喜欢甜品.现从这两个系的学生中,各随机抽取
名不喜欢甜品.现从这两个系的学生中,各随机抽取![]() 人,记抽出的
人,记抽出的![]() 人中不喜欢甜品的人数为
人中不喜欢甜品的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是预测到的某地5月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择5月1日至5月13日中的某一天到达该市,并停留2天 
(1)求此人到达当日空气质量优良的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着支付宝、微信等支付方式的上线,越来越多的商业场景可以实现手机支付.有关部门为了了解各年龄段的人使用手机支付的情况,随机调查了50次商业行为,并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
手机支付 | 4 | 6 | 10 | 6 | 2 | 0 |
(1)若把年龄在![]() 的人称为中青年,年龄在
的人称为中青年,年龄在![]() 的人称为中老年,请根据上表完成以下
的人称为中老年,请根据上表完成以下![]() 列联表;并判断是否可以在犯错误的概率不超过0.05的前提下,认为使用手机支付与年龄(中青年、中老年)有关系?
列联表;并判断是否可以在犯错误的概率不超过0.05的前提下,认为使用手机支付与年龄(中青年、中老年)有关系?
手机支付 | 未使用手机支付 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
(2)若从年龄在![]() 的被调查中随机选取2人进行调查,记选中的2人中,使用手机支付的人数为
的被调查中随机选取2人进行调查,记选中的2人中,使用手机支付的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:![]() ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.15 | 0.10 | 0.005 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,互不相同的点A1 , A2 , …,An , …和B1 , B2 , …,Bn , …分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等,设OAn=an , 若a1=1,a2=2,则数列{an}的通项公式是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面
平面![]() ,
,![]() .则下列命题中正确的有_____.(填序号)
.则下列命题中正确的有_____.(填序号)
①PB⊥AD;
②平面PAB⊥平面PAE;
③BC∥平面PAE;
④直线PD与平面ABC所成的角为45°.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月15日,天宫二号实验室发射成功.借天宫二号东风,某厂推出品牌为“玉兔”的新产品.生产“玉兔”的固定成本为20000元,每生产一件“玉兔”需要增加投入100元.根据初步测算,总收益(单位:元)满足分段函数![]() ,其中
,其中 ,
,![]() 是“玉兔”的月产量(单位:件),总收益=总成本+利润.
是“玉兔”的月产量(单位:件),总收益=总成本+利润.
(I)试将利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(II)当月产量为多少件时利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面是边长为 ![]() 的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2 ![]() ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点. 
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角A﹣MN﹣Q的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com