
【题目】单位圆的内接正n(n≥3)边形的面积记为![]() ,则f(3)=_____; 下面是关于
,则f(3)=_____; 下面是关于![]() 的描述:
的描述:
③![]()
![]() ④
④![]()
![]()
![]()
其中正确结论的序号为__________.(注:请写出所有正确结论的序号)
【答案】 ![]() ①③④
①③④
【解析】半径为1的圆的内接正n边形的边长为2sin![]() ,
,
边心距为cos![]() ,
,
则正n边形的面积为f(n)=n![]() 2sin
2sin![]() cos
cos![]() =
=![]() sin
sin![]() ,
,
可得f(3)=![]() sin
sin![]() =
=![]() ;
;
考虑函数f(x)=![]() sin
sin![]() ,x>2,且x∈N,
,x>2,且x∈N,
可得导数f′(x)=![]() sin
sin![]() ﹣
﹣![]() cos
cos![]() ,
,
当x=3,4时,f′(x)>0成立;
当x>4,且x∈N,0<![]() <
<![]() ,
,
有0<sin![]() <1,0<cos
<1,0<cos![]() <1,
<1,
且sin![]() <
<![]() <tan
<tan![]() ,
,
可得![]() sin
sin![]() >
>![]() cos
cos![]() ,
,
可得f′(x)>0,
则f(x)在x>2,且x∈N,为增函数,
则f(n)<f(n+1);
由于f(n)为增函数,且sin![]() <
<![]() ,0<
,0<![]() <
<![]() ,
,
可得f(n)<![]()
![]() =π,
=π,
即f(n)取不到π;
又f(n)﹣f(2n)=![]() sin
sin![]() ﹣nsin
﹣nsin![]() =nsin
=nsin![]() cos
cos![]() ﹣nsin
﹣nsin![]()
=nsin![]() (cos
(cos![]() ﹣1)<0,即f(n)<f(2n);
﹣1)<0,即f(n)<f(2n);
由f(2n)﹣2f(n)=nsin![]() ﹣2
﹣2![]() sin
sin![]() =nsin
=nsin![]() (1﹣2cos
(1﹣2cos![]() ),
),
由于n≥3,可得![]() ≤cos
≤cos![]() <1,
<1,
可得f(2n)﹣2f(n)≤0,
即f(2n)≤2f(n).
综上可得,正确结论序号为①③④.
故填![]() ;①③④.
;①③④.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图如图所示,图中从左到右各小长方形面积之比为![]() ,第二小组频数为12.
,第二小组频数为12.
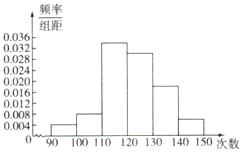
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,试估计该校全体高一学生的达标率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年1月,《中国青年报》社会调查中心联合问卷网,对多人进行了一项关于“二十四节气”的调查,请选择合适的图表分别表示以下调查结果:
(1)全部都知道、大部分知道、少部分知道和完全不知道“二十四节气”日期的受访者分别占12.6%、49.0%、34.6%和3.8%;
(2)调查显示,受访者最敏感的节气是立春(50.9%)、冬至(46.4%)和清明(43.9%).其他依次为:立冬(32.2%)、立秋(32.1%)、立夏(29.6%)、夏至(28.5%)、大暑(20.7%)、惊蛰(18.8%)、春分(18.7%)、雨水(18.7%)、大寒(16.4%)、大雪(15.3%)、秋分(14.8%)、小暑(14.0%)、芒种(12.2%)、小满(11.6%)、处暑(11.6%)、白露(11.3%)、霜降(10.7%)和小雪(10.5%).最不敏感的节气是谷雨(10.4%)、小寒(9.7%)和寒露(7.9%).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
(3)求函数![]() 在定义域上的最大值及最小值,并求出函数取最值时
在定义域上的最大值及最小值,并求出函数取最值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占80%.现从参与调查的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第1组
人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
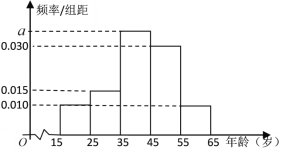
(1)求![]() 的值;
的值;
(2)求出样本的平均数(同一组数据用该区间的中点值作代表);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行问卷调查,求第2组中抽到
人进行问卷调查,求第2组中抽到![]() 人的概率.
人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表:
![]()
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程![]() ,其中
,其中![]() =
= ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com