
【题目】给出如下四个命题:①e ![]() >2②ln2>
>2②ln2> ![]() ③π2<3π④
③π2<3π④ ![]() <
< ![]() ,正确的命题的个数为( )
,正确的命题的个数为( )
A.1
B.2
C.3
D.4
科目:高中数学 来源: 题型:
【题目】根据函数f(x)=log2x的图象和性质解决以下问题:
(1)若f(a)>f(2),求a的取值范围;
(2)y=log2(2x-1)在[2,14]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次函数![]() ,分别从集合
,分别从集合![]() 和
和![]() 中随机取一个数
中随机取一个数![]() 和
和![]() 得到数对
得到数对![]() .
.
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 在
在![]() 内是偶函数的概率;
内是偶函数的概率;
(2)若![]() ,
, ![]() ,求函数
,求函数![]() 有零点的概率;
有零点的概率;
(3)若![]() ,
, ![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.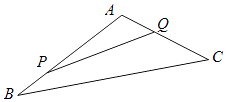
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,AP段围墙造价为每平方米150元,AQ段围墙造价为每平方米100元.若围围墙用了30000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=. ![]() ,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2 .
(Ⅰ)求函数h(x)=f(x)﹣3x的极值;
(Ⅱ)若函数g(x)=f(x)﹣ax在定义域内为增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为 ![]() (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣ ![]() ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E、F分别是BB1、CD的中点.
(1)求证:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是长轴长为 ![]() 的椭圆Q:
的椭圆Q: ![]() 上异于顶点的一个动点,O为坐标原点,A为椭圆的右顶点,点M为线段PA的中点,且直线PA与OM的斜率之积恒为
上异于顶点的一个动点,O为坐标原点,A为椭圆的右顶点,点M为线段PA的中点,且直线PA与OM的斜率之积恒为 ![]() .
.
(1)求椭圆Q的方程;
(2)设过左焦点F1且不与坐标轴垂直的直线l交椭圆于C,D两点,线段CD的垂直平分线与x轴交于点G,点G横坐标的取值范围是 ![]() ,求|CD|的最小值.
,求|CD|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com