
【题目】已知多面体![]() 如图所示,底面
如图所示,底面![]() 为矩形,其中
为矩形,其中![]() 平面
平面![]() ,
, ![]() .若
.若![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() ,
, ![]() 的中点,其中
的中点,其中![]() .
.
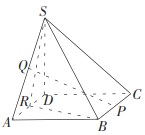
(Ⅰ)证明: ![]() ;
;
(Ⅱ)若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
【答案】(I)详见解析;(II)![]() .
.
【解析】试题分析:
(1)利用题意证得![]() 平面
平面![]() ,然后利用线面垂直的性质和直线平行的结论可得
,然后利用线面垂直的性质和直线平行的结论可得![]() .
.
(2)建立空间直角坐标系,由平面向量的法向量和二面角的余弦值可求得![]() 的长为
的长为![]() .
.
试题解析:
(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
,
因为![]() 是正方形,所以
是正方形,所以![]()
![]()
![]() ,
, ![]() ;
;
因为![]() 分别是
分别是![]() ,
, ![]() 的中点,所以
的中点,所以![]()
![]()
![]() ,
, ![]() ;
;
又因为![]()
![]()
![]() 且
且![]() ,所以
,所以![]()
![]()
![]() ,
, ![]() ,
,
所以四边形![]() 是平行四边形, 所以
是平行四边形, 所以![]()
![]()
![]() .
.
因为![]()
![]() 平面
平面![]() ,
,
又![]() 故
故![]() ,故
,故![]() .
.
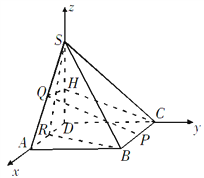
(Ⅱ)如图,以D为原点,射线DA,DC,DS分别为x,y,z轴正方向,建立空间直角坐标系;设![]() (
(![]() ),则
),则![]() .
.
因为![]() ⊥底面
⊥底面![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面SRB的一个法向量为![]() ,
,
![]() ,
, ![]() ,则
,则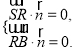 即
即![]()
令x=1,得![]() ,所以
,所以![]() ,
,
由已知,二面角![]() 的余弦值为
的余弦值为![]() ,
,
所以得 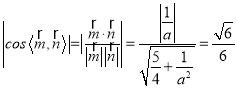 ,解得a =2,所以SD=2.
,解得a =2,所以SD=2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某学生每次投篮的命中概率都为![]() .现采用随机模拟的方法求事件的概率:先由计算器产生0到9之间的整数值随机数,制定1、2、3、4表示命中,5、6、7、8、9、0表示不命中;再以每3个随机数为一组,代表三次投篮的结果.经随机模拟产生如下20组随机数:989 537 113 730 488 556 027 393 257 431 683 569 458 812 932 271 925 191 966 907,据此统计,该学生三次投篮中恰有一次命中的概率约为__________.
.现采用随机模拟的方法求事件的概率:先由计算器产生0到9之间的整数值随机数,制定1、2、3、4表示命中,5、6、7、8、9、0表示不命中;再以每3个随机数为一组,代表三次投篮的结果.经随机模拟产生如下20组随机数:989 537 113 730 488 556 027 393 257 431 683 569 458 812 932 271 925 191 966 907,据此统计,该学生三次投篮中恰有一次命中的概率约为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算与求解
(1)计算:2log32﹣log3 ![]() +log38﹣5
+log38﹣5 ![]() ;
;
(2)已知a>0,a≠1,若loga(2x+1)<loga (4x﹣3),求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1﹣ ![]() (a>0且a≠1)是定义在R上的奇函数.
(a>0且a≠1)是定义在R上的奇函数.
(1)求a的值;
(2)求f(x)的值域;
(3)若关于x的方程|f(x)(2x+1)|=m有1个实根,求实数m的取值范围;
(4)当x∈(0,1]时,tf(x)≥2x﹣2恒成立,求实数t取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入,已知研发投入![]() (十万元)与利润
(十万元)与利润![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系。试求:
呈线性相关关系。试求:
(1)线性回归方程![]() ;
;
(2)估计![]() 时,利润是多少?
时,利润是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:
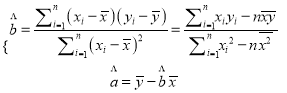
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com