已知数列{an},an=pn+λqn(p>0,q>0,p≠q,λ∈R,λ≠0,n∈N*).
(1)求证:数列{an+1-pan}为等比数列;
(2)数列{an}中,是否存在连续的三项,这三项构成等比数列?试说明理由;
(3)设A={(n,bn)|bn=3n+kn,n∈N*},其中k为常数,且k∈N*,B={(n,cn)|cn=5n,n∈N*},求A∩B.
【答案】
分析:(1)根据a
n=p
n+λq
n可得a
n+1-pa
n的表达式,整理可得
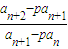
为常数,进而可判断数列{a
n+1-pa
n}为等比数列.
(2)取数列{a
n}的连续三项a
n,a
n+1,a
n+2把a
n=p
n+λq
n代入a
n+12-a
na
n+2整理可知结果不为0,进而可判断a
n+12≠a
na
n+2,即数列{a
n}中不存在连续三项构成等比数列;
(3)由3
n+2
n=5
n整理得
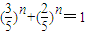
,设
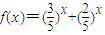
则可知f(x)为减函数,故可判定f(x)=1的解只有一个,从而当且仅当n=1,3
n+2
n=5
n成立,同样的道理可证当k=1,k=3或k≥5时,B∩C=∅;当k=2时,B∩C={(1,5)},当k=4时,B∩C={(2,25)}.
解答:解:(1)∵a
n=p
n+λq
n,
∴a
n+1-pa
n=p
n+1+λq
n+1-p(p
n+λq
n)=λq
n(q-p),
∵λ≠0,q>0,p≠q
∴
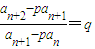
为常数
∴数列{a
n+1-pa
n}为等比数列
(2)取数列{a
n}的连续三项a
n,a
n+1,a
n+2(n≥1,n∈N
*),
∵a
n+12-a
na
n+2=(p
n+1+λq
n+1)
2-(p
n+λq
n)(p
n+2+λq
n+2)=-λp
nq
n(p-q)
2,
∵p>0,q>0,p≠q,λ≠0,
∴-λp
nq
n(p-q)
2≠0,即a
n+12≠a
na
n+2,
∴数列{a
n}中不存在连续三项构成等比数列;
(3)当k=1时,3
n+k
n=3
n+1<5
n,此时B∩C=∅;
当k=3时,3
n+k
n=3
n+3
n=2•3
n为偶数;而5
n为奇数,此时B∩C=∅;
当k≥5时,3
n+k
n>5
n,此时B∩C=∅;
当k=2时,3
n+2
n=5
n,发现n=1符合要求,
下面证明唯一性(即只有n=1符合要求).
由3
n+2
n=5
n得
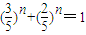
,
设
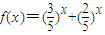
,则
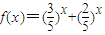
是R上的减函数,
∴f(x)=1的解只有一个
从而当且仅当n=1时
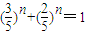
,
即3
n+2
n=5
n,此时B∩C={(1,5)};
当k=4时,3
n+4
n=5
n,发现n=2符合要求,
下面同理可证明唯一性(即只有n=2符合要求).
从而当且仅当n=2时
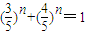
,
即3
n+4
n=5
n,此时B∩C={(2,25)};
综上,当k=1,k=3或k≥5时,B∩C=∅;
当k=2时,B∩C={(1,5)},
当k=4时,B∩C={(2,25)}.
点评:本题主要考查了等比数列的确定和集合的相关知识.考查了学生分析和运算能力.

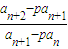 为常数,进而可判断数列{an+1-pan}为等比数列.
为常数,进而可判断数列{an+1-pan}为等比数列.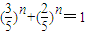 ,设
,设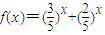 则可知f(x)为减函数,故可判定f(x)=1的解只有一个,从而当且仅当n=1,3n+2n=5n成立,同样的道理可证当k=1,k=3或k≥5时,B∩C=∅;当k=2时,B∩C={(1,5)},当k=4时,B∩C={(2,25)}.
则可知f(x)为减函数,故可判定f(x)=1的解只有一个,从而当且仅当n=1,3n+2n=5n成立,同样的道理可证当k=1,k=3或k≥5时,B∩C=∅;当k=2时,B∩C={(1,5)},当k=4时,B∩C={(2,25)}.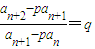 为常数
为常数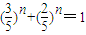 ,
,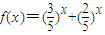 ,则
,则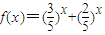 是R上的减函数,
是R上的减函数,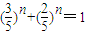 ,
,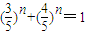 ,
,
