
【题目】函数f(x)=Asin(x+)(A>0,>0,0<<)的部分图象如图所示,又函数g(x)=f(x+![]() ).
).
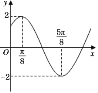
(1)求函数g(x)的单调增区间;
(2)设![]() ABC的内角ABC的对边分别为abc,又c=
ABC的内角ABC的对边分别为abc,又c=![]() ,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
科目:高中数学 来源: 题型:
【题目】哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召,实施网络授课,为检验学生上网课的效果,高三学年进行了一次网络模拟考试.全学年共1500人,现从中抽取了100人的数学成绩,绘制成频率分布直方图(如下图所示).已知这100人中![]() 分数段的人数比
分数段的人数比![]() 分数段的人数多6人.
分数段的人数多6人.
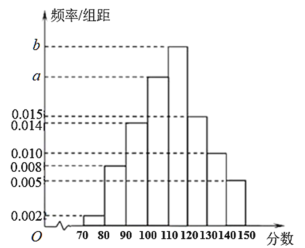
(1)根据频率分布直方图,求a,b的值,并估计抽取的100名同学数学成绩的中位数;
(2)现用分层抽样的方法从分数在![]() ,
,![]() 的两组同学中随机抽取6名同学,从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言,求这2名同学的分数不在同一组内的概率.
的两组同学中随机抽取6名同学,从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言,求这2名同学的分数不在同一组内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 经过点
经过点![]() ,且动圆
,且动圆![]() 被
被![]() 轴截得的弦长为4,记圆心
轴截得的弦长为4,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)过![]() 轴下方一点
轴下方一点![]() 向曲线
向曲线![]() 作切线,切点记作
作切线,切点记作![]() 、
、![]() ,直线
,直线![]() 交曲线
交曲线![]() 于点
于点![]() ,若直线
,若直线![]() 、
、![]() 的斜率乘积为
的斜率乘积为![]() ,点
,点![]() 在以
在以![]() 为直径的圆上,求点
为直径的圆上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务时间的统计数据如下:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)从该校学生中随机调查60名学生,一周参加社区服务时间超过1小时的人数记为X,以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,求X的分布列和数学期望.
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校高三年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论:
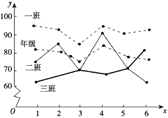
①一班成绩始终高于年级平均水平,整体成绩比较好;
②二班成绩不够稳定,波动程度较大;
③三班成绩虽然多次低于年级平均水平,但在稳步提升.
其中错误的结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 是椭圆与
是椭圆与![]() 轴负半轴的交点,经过
轴负半轴的交点,经过![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,经过
,经过![]() 且与
且与![]() 平行的直线与椭圆交于点
平行的直线与椭圆交于点![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎蔓延全国,作为主要战场的武汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体现了中国速度.随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其占地是出一个正方形和四个以正方形的边为底边、腰长为400m的等腰三角形组成的图形(如图所示),为使占地面积最大,则等腰三角形的底角为( )
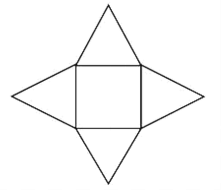
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为阻隔新冠肺炎病毒,多地进行封城.封城一段时间后,有的人情绪波动不大,反应一般;也有的人情绪波动大,反应强烈.某社区为了解民众心理反应,随机调查了100位居民,得到数据如下表:
反应强烈 | 反应一般 | 合计 | |
男 | 20 | 20 | 40 |
女 | 45 | 15 | 60 |
合计 | 65 | 35 | 100 |
(1)以这100个人的样本数据估计该市的总体数据,且以频率估计概率,若从该社区的男性居民中随机抽取3位,记其中反应强烈的人数为X,求随机变量X的分布列和数学期望;
(2)根据调查数据,能否在犯错的概率不超过![]() 的前提下认为“反应强烈”与性别有关,并说明理由.
的前提下认为“反应强烈”与性别有关,并说明理由.
参考数据:
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
(参考公式: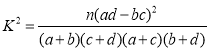 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com