
【题目】设点P是函数![]() 图象上任意一点,点Q坐标为
图象上任意一点,点Q坐标为![]() ,当
,当![]() 取得最小值时圆
取得最小值时圆![]() 与圆
与圆![]() 相外切,则
相外切,则![]() 的最大值为
的最大值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题意,分析函数y![]() 的解析式可得(x﹣1)2+y2=4,(y≤0),分析可得其对应的曲线为圆心在C(1,0),半径为2的圆的下部分,由Q的坐标可得Q在直线x﹣2y﹣6=0上,据此分析可得当|PQ|取得最小值时,PQ与直线x﹣2y﹣6=0垂直,此时有
的解析式可得(x﹣1)2+y2=4,(y≤0),分析可得其对应的曲线为圆心在C(1,0),半径为2的圆的下部分,由Q的坐标可得Q在直线x﹣2y﹣6=0上,据此分析可得当|PQ|取得最小值时,PQ与直线x﹣2y﹣6=0垂直,此时有![]() 2,解可得a的值,即可得圆C1的方程,结合两圆外切的性质可得
2,解可得a的值,即可得圆C1的方程,结合两圆外切的性质可得![]() 3+2=5,变形可得(m+n)2=25,由基本不等式的性质分析可得答案.
3+2=5,变形可得(m+n)2=25,由基本不等式的性质分析可得答案.
根据题意,函数y![]() ,即(x﹣1)2+y2=4,(y≤0),
,即(x﹣1)2+y2=4,(y≤0),
对应的曲线为圆心在C(1,0),半径为2的圆的下半部分,
又由点Q(2a,a﹣3),则Q在直线x﹣2y﹣6=0上,
当|PQ|取得最小值时,PQ与直线x﹣2y﹣6=0垂直,此时有![]() 2,解可得a=1,
2,解可得a=1,
圆C1:(x﹣m)2+(y+2)2=4与圆C2:(x+n)2+(y+2)2=9相外切,
则有![]() 3+2=5,
3+2=5,
变形可得:(m+n)2=25,
则mn![]() ,
,
故选:C.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
【题目】汽车是碳排放量比较大的交通工具,某地规定,从2017年开始,将对二氧化碳排放量超过130 g/km的轻型汽车进行惩罚性征税,检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为![]() =120 g/km.
=120 g/km.
(1)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性;
(2)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过130 g/km的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届安徽省合肥市高三第一次教学质量检测】一家大型购物商场委托某机构调查该商场的顾客使用移动支付的情况.调查人员从年龄在![]() 内的顾客中,随机抽取了180人,调查结果如表:
内的顾客中,随机抽取了180人,调查结果如表:

(1)为推广移动支付,商场准备对使用移动支付的顾客赠送1个环保购物袋.若某日该商场预计有12000人购物,试根据上述数据估计,该商场当天应准备多少个环保购物袋?
(2)某机构从被调查的使用移动支付的顾客中,按分层抽样的方式抽取7人作跟踪调查,并给其中2人赠送额外礼品,求获得额外礼品的2人年龄都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
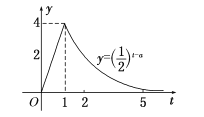
(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接第二届国际互联网大会,组委会对报名参加服务的![]() 名志愿者进行互联网知识测试,从这
名志愿者进行互联网知识测试,从这![]() 名志愿者中采用随机抽样的方法抽取
名志愿者中采用随机抽样的方法抽取![]() 人,所得成绩如下:
人,所得成绩如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)作出抽取的![]() 人的测试成绩的茎叶图,以频率为概率,估计这
人的测试成绩的茎叶图,以频率为概率,估计这![]() 志愿者中成绩不低于
志愿者中成绩不低于![]() 分的人数;
分的人数;
(2)从抽取的成绩不低于![]() 分的志愿者中,随机选
分的志愿者中,随机选![]() 名参加某项活动,求选取的
名参加某项活动,求选取的![]() 人恰有一人成绩不低于
人恰有一人成绩不低于![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 、
、![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 和曲线
和曲线![]() 只有一个交点,求
只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2-2mx-4my+5m2-4=0(m∈R),圆C2:x2+y2=1.
(1)过定点M(1,-2)作圆C2的切线,求切线的方程;
(2)若圆C1与圆C2相交,求m的取值范围;
(3)已知点P(2,0),圆C1上一点A,圆C2上一点B,求|![]() |的最小值的取值范围.
|的最小值的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com